[F] [X] [W] [L]

تطور جملة ميكانيكيـة. تطبيقات قوانين نيوتن

تُعنى دراسة تطور جملة ميكانيكية بفهم كيفية تغير الحركة، والقوى المؤثرة على جسم، أو جملة ميكانيكية مع مرور الزمن. يعتمد تحليل تطور الجملة على القوانين الأساسية لميكانيكا نيوتن، مثل قانون الحركة، وقانون حفظ الطاقة. الجملة الميكانيكية قد تتكون من أجسام صلبة، جسيمات منفردة، أو أنظمة معقدة متعددة المكونات.

تُستخدم دراسة تطور الجملة الميكانيكية لفهم ديناميكيات الحركة في العديد من المجالات، مثل الهندسة الميكانيكية، الفيزياء النظرية، والتطبيقات الصناعية.

تحليل تطور الجملة يعتمد أيضًا على أدوات رياضية متقدمة، مثل قوانين التحليل العددي، وحساب التفاضل والتكامل.

ملاحظة: توجد وثيقة التلميذ بصيغة الـ PDF في نهاية المقال

I ـ تذكير:

عرف كل من: المسار، المرجع ؟

أ ـ تعريف المسار: 

هو مجموعة النقاط التي يشغلها المتحرك خلال حركته

ب ـ تعريف المرجع: 

هو جسم صلب تنسب اليه الحركة، و يمكن أن يكون ساكنا، أو متحركا، ويرتبط بمعلمين: معلم المسافة ومعلم الزمن.

وضح مفهوم المرجع العطالي (الغاليلي) ؟

هو كل مرجع يتحقق فيه مبدا العطالة.

II ـ مميزات الحركة:

1 ـ شعاع الموضع و شعاع الانتقال:

ـ عرف شعاع الموضع ؟ 

ـ أكتب عبارته الشعاعية ؟ 

ـ مثله في معلم ؟

أ ـ تعريف شعاع الموضع: 

هو شعاع يحدد موضع المتحرك خلال لحظة زمنية معينة ونعبر عنه بالعبارة التالية:

$$\vec{r}=\overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}$$

 وذلك كما يوضحه التمثيل التالي:

ـ عرف شعاع الانتقال ومثله بين موضعين مختلفين ؟

ب ـ تعريف شعاع الانتقال: 

هو شعاع يعبر عن انتقال المتحرك من موضع الى موضع اخر  ونعبر عن شعاع الانتقال بالعبارة التالية:

$\mathrm{\Delta }\overrightarrow{r}=\overrightarrow{r_2}-\overrightarrow{r_1}$

ومنه: $\mathrm{\Delta }\overrightarrow{r}=(x_2-x_1)\overrightarrow{i}+(y_2-y_1)\overrightarrow{j}+(z_2-z_1)\overrightarrow{k}$

كما يوضحه التمثيل التالي:

2 ـ شعاع السرعة:

ـ عرف السرعة؟ 

ـ أكتب عبارة شعاع السرعة المتوسطة وكذلك عبارة شعاع السرعة اللحظية ؟

تعريف السرعة:

هي تغير المسافة بالنسبة للزمن

نعبر عن شعاع السرعة المتوسطة بالعبارة:

${\overrightarrow{v}}_m=\frac{\mathrm{\Delta }\overrightarrow{r}}{\mathrm{\Delta }t}$

ومنه: ${\overrightarrow{v}}_m=\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}\overrightarrow{i}+\frac{\mathrm{\Delta }y}{\mathrm{\Delta }t}\overrightarrow{j}+\frac{\mathrm{\Delta }z}{\mathrm{\Delta }t}\overrightarrow{k}$

نعبر عن السرعة اللحظية بالعبارة:

$\overrightarrow{v}=\underset{\mathrm{\Delta }t\to 0}{lim}\left({\overrightarrow{v}}_m\right)$

ومنه: $\overrightarrow{v}=\underset{\mathrm{\Delta }t\to 0}{lim}\left(\frac{\mathrm{\Delta }\overrightarrow{r}}{\mathrm{\Delta }t}\right)$

ومنه: $\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}$

ومنه: $\overrightarrow{v}=\frac{dx}{dt}\overrightarrow{i}+\frac{dy}{dt}\overrightarrow{j}+\frac{dz}{dt}\overrightarrow{k}$

ولدينا: $\frac{dx}{dt}=v_x$, $\frac{dy}{dt}=v_y$, و $\frac{dz}{dt}=v_z$

ومنه: $\overrightarrow{v}=v_x\overrightarrow{i}+v_y\overrightarrow{j}+v_z\overrightarrow{k}$

ومنه: $v=\sqrt{v_x^2+v_y^2+v_z^2}$

3 ـ شعاع التسارع:

ـ عرف التسارع ؟

هو عبارة عن تغير السرعة بدلالة تغير الزمن 

ـ أكتب عبارات كل من شعاعي التسارع المتوسط (الوسطي)، التسارع اللحظي. 

ـ أكتب عبارة التسارع الناظمي ؟

أ ـ عبارة شعاع التسارع المتوسط:

اذا انتقل متحرك من نقطة  M الى نقطة  M' وتغيرت سرعته بين الموضعين نقول ان الجسم اصبح له تسارع  نعبر عنه بالعبارة:

${\overrightarrow{a}}_m=\frac{\mathrm{\Delta }\overrightarrow{v}}{\mathrm{\Delta }t}$

ومنه: ${\overrightarrow{a}}_m=\frac{\mathrm{\Delta }{v}_x}{\mathrm{\Delta }t}\overrightarrow{i}+\frac{\mathrm{\Delta }{v}_y}{\mathrm{\Delta }t}\overrightarrow{j}+\frac{\mathrm{\Delta }{v}_z}{\mathrm{\Delta }t}\overrightarrow{k}$

ب ـ عبارة شعاع التسارع اللحظي:

نعبر عن التسارع اللحظي بالعبارة:

$\overrightarrow{a}=\underset{\mathrm{\Delta }t\to 0}{lim}\left({\overrightarrow{a}}_m\right)$

ومنه: $\overrightarrow{a}=\underset{\mathrm{\Delta }t\to 0}{lim}\left(\frac{\mathrm{\Delta }\overrightarrow{v}}{\mathrm{\Delta }t}\right)$

ومنه: $\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$

ومنه: $\overrightarrow{a}=\frac{d{v}_x}{dt}\overrightarrow{i}+\frac{d{v}_y}{dt}\overrightarrow{j}+\frac{d{v}_z}{dt}\overrightarrow{k}$

ولدينا: $\frac{d{v}_x}{dt}=a_x$, $\frac{d{v}_y}{dt}=a_y$, و $\frac{d{v}_z}{dt}=a_z$

ومنه: $\overrightarrow{a}=a_x\overrightarrow{i}+a_y\overrightarrow{j}+a_z\overrightarrow{k}$

ومنه: $a=\sqrt{a_x^2+a_y^2+a_z^2}$

ملاحظة: يمكن الاعتماد على النشاط التالي من أجل دراسة كل العناصر السابقة

نشاط

نعتبر متحرك نقطي يتحرك وفق مسار معين في مرجع نعتبره مرجع عطالي (غاليلي) مرتبط بمعلمين :معلم المسافة و معلم الزمن ، نعبر عن موضع المتحرك في كل لحظة بشعاع الموضع:

$\overrightarrow{r}=3\overrightarrow{i}+(10t)\overrightarrow{j}+(-4,9t^2+17,32t)\overrightarrow{k}$

فينتقل وفق شعاع الانتقال من موضع الى موضع اخر، نأخذ الزمن بالثانية (s) و المسافة بالمتر (m).

1 ـ اشرح العبارات التي تحتها سطر ؟

2 ـ أكتب عبارة شعاع الموضع في الحالة العامة ثم عبارات أشعة المواضع عند اللحظات الزمنية

t₀ = 0 (s) ، t₁ = 0,5 (s) ، t₂ = 1 (s) و استنتج طويلة كل منها و مثلهما في معلم متعامد و متجانس

$$(O,\vec{i},\vec{j},\vec{k})$$

نأخذ مقياس الرسم: 1 cm → 2 m من أجل تمثيل الاحداثيات.

3 ـ أنشئ مسار كيفي يمر عبر المواقع المحددة سابقا ؟

4 ـ مثل شعاع الانتقال بين الموضعين الموافقين للحظتين t₁ ، t₂ ثم أكتب عبارته واستنتج طويلته ؟

5 ـ أكتب عبارة شعاع السرعة المتوسطة بين اللحظتين t₁ ، t₂ و استنتج طويلته ثم مثله ؟

نأخذ مقياس الرسم : 1 cm → 10 (m/s)

6 ـ  أكتب عبارة شعاع السرعة اللحظية عند اللحظتين t₁ ، t₂ ثم استنتج طويلة في كل لحظة ؟

7 ـ أكتب عبارة شعاع التسارع المتوسط (الوسطي) بين اللحظتين t₁ ، t₂ و استنتج طويلته ؟

8 ـ أكتب عبارة شعاع التسارع اللحظي و استنتج طويلته ثم مثله في لحظة تختارها ؟

نأخذ مقياس الرسم 1 cm → 4,9 (m/s²)

الاجابة:

1 ـ شرح العبارات التي تحتها سطر:

المسار: هو مجموعة النقاط التي يشغلها المتحرك خلال حركته

المرجع: هو جسم صلب تنسب اليه الحركة ، و يمكن أن يكون ساكنا أو متحركا

المرجع العطالي (الغاليلي): هو كل مرجع يتحقق فيه مبدا العطالة

شعاع الموضع: هو شعاع يحدد موضع المتحرك خلال لحظة زمنية معينة

شعاع الانتقال: هو شعاع يعبر عن انتقال المتحرك من موضع الى موضع اخر

2 ـ عبارة شعاع الموضع في الحالة العامة:

$\overrightarrow{r}=\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$

ـ عبارات شعاع الموضع عند اللحظات الزمنية t₀ = 0 (s) ، t₁ = 0,5 (s) ، t₂ = 1 (s) t₂ = 1 (s):

نعبر عن المتجهات بالعبارات التالية:

${\overrightarrow{r}}_0=3\overrightarrow{i}\text{(m)}$

${\overrightarrow{r}}_1=3\overrightarrow{i}+5\overrightarrow{j}+7,44\overrightarrow{k}$

${\overrightarrow{r}}_2=3\overrightarrow{i}+10\overrightarrow{j}+12,42\overrightarrow{k}$

ـ استنتاج طويلات أشعة الموضع:

$r_0=\sqrt{3^2}=3\text{(m)}$

$r_1=\sqrt{3^2+5^2+{7.44}^2}=9.45\text{(m)}$

$r_2=\sqrt{3^2+{10}^2+{12.42}^2}=16.22\text{(m)}$

ـ تمثيل أشعة الموضع: (أنظر الشكل)

3 ـ انشاء مسار كيفي يمر عبر المواقع المحددة سابقا :(أنظر الشكل السابق)

4 ـ تمثيل شعاع الانتقال: (أنظر الشكل السابق)

كتابة عبارة شعاع الانتقال بين الموضعين الموافقين للحظتين t₁ ، t₂:

نعبر عن شعاع الانتقال بالعبارة التالية: $\overrightarrow{\mathrm{\Delta }r}=\overrightarrow{r_2}-\overrightarrow{r_1}$

وبالتالي: $\overrightarrow{\mathrm{\Delta }r}=(x_2-x_1)\overrightarrow{i}+(y_2-y_1)\overrightarrow{j}+(z_2-z_1)\overrightarrow{k}$

وبالتعويض بالقيم المعطاة: $\overrightarrow{\mathrm{\Delta }r}=(3-3)\overrightarrow{i}+(10-5)\overrightarrow{j}+(12.42-7.44)\overrightarrow{k}$

فنحصل على: $\overrightarrow{\mathrm{\Delta }r}=5\overrightarrow{j}+4.98\overrightarrow{k}\text{(m)}$

5 ـ كتابة عبارة شعاع السرعة المتوسطة بين اللحظتين t₁ ، t₂: 

نعبر عن شعاع السرعة المتوسطة بالعبارة: ${\overrightarrow{v}}_m=\frac{\overrightarrow{\mathrm{\Delta }r}}{\mathrm{\Delta }t}$

ومنها: ${\overrightarrow{v}}_m=\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}\overrightarrow{i}+\frac{\mathrm{\Delta }y}{\mathrm{\Delta }t}\overrightarrow{j}+\frac{\mathrm{\Delta }z}{\mathrm{\Delta }t}\overrightarrow{k}$

وبالتعويض بالقيم المعطاة: ${\overrightarrow{v}}_{12}=\frac{(3-3)}{(1-0,5)}\overrightarrow{i}+\frac{(10-5)}{(1-0,5)}\overrightarrow{j}+\frac{(12,42-7,44)}{(1-0,5)}\overrightarrow{k}$

فنحصل على: ${\overrightarrow{v}}_{12}=10\overrightarrow{j}+9,96\overrightarrow{k}\text{(m/s)}$

استنتاج طويلة شعاع السرعة المتوسطة: $v_{12}=\sqrt{{10}^2+9,{96}^2}=14,11\text{(m/s)}$

تمثيل شعاع السرعة المتوسطة: ( أنظر الشكل السابق)

6 ـ كتابة عبارة شعاع السرعة اللحظية عند اللحظتين t₁ ، t₂: 

نعبر عن السرعة اللحظية بالعبارة: $\overrightarrow{v}=\underset{\mathrm{\Delta }t\to 0}{lim}\left({\overrightarrow{v}}_m\right)$

ومنه: $\overrightarrow{v}=\underset{\mathrm{\Delta }t\to 0}{lim}\left(\frac{\overrightarrow{\mathrm{\Delta }r}}{\mathrm{\Delta }t}\right)$

ومنه: $\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}$

ومنه: $\overrightarrow{v}=\frac{dx}{dt}\overrightarrow{i}+\frac{dy}{dt}\overrightarrow{j}+\frac{dz}{dt}\overrightarrow{k}$

حيث: $\frac{dx}{dt}=v_x$, $\frac{dy}{dt}=v_y$, و $\frac{dz}{dt}=v_z$

ومنه: $\overrightarrow{v}=\frac{d(3)}{dt}\overrightarrow{i}+\frac{d(10t)}{dt}\overrightarrow{j}+\frac{d(-4,9t^2+17,32t)}{dt}\overrightarrow{k}$

فنحصل على: $\overrightarrow{v}=10\overrightarrow{j}+(-9,8t+17,32)\overrightarrow{k}$

من أجل $t_1=0,5$ (s) نجد: ${\overrightarrow{v}}_1=10\overrightarrow{j}+12,42\overrightarrow{k}$

ومن أجل $t_2=1$ (s) نجد: ${\overrightarrow{v}}_2=10\overrightarrow{j}+7,52\overrightarrow{k}$

استنتاج طويلة شعاع السرعة اللحظية في كل لحظة:

من أجل $t_1=0,5$ (s): $v_1=\sqrt{{10}^2+12,{42}^2}=15,94\text{m/s}$

من أجل $t_2=1$ (s): $v_2=\sqrt{{10}^2+7,{52}^2}=12,51\text{m/s}$

7 ـ أكتب عبارة شعاع التسارع المتوسط (الوسطي) بين اللحظتين t₁ ، t₂:

اذا انتقل متحرك من نقطة M₁ الى نقطة M₂ وتغيرت سرعته بين الموضعين نقول أن المتحرك أصبح له تسارع نعبر عنه بالعبارة : 

نعبر عن التسارع المتوسط بالعبارة: ${\overrightarrow{a}}_m=\frac{\mathrm{\Delta }\overrightarrow{v}}{\mathrm{\Delta }t}$

ومنها: ${\overrightarrow{a}}_m=\frac{\mathrm{\Delta }{v}_x}{\mathrm{\Delta }t}\overrightarrow{i}+\frac{\mathrm{\Delta }{v}_y}{\mathrm{\Delta }t}\overrightarrow{j}+\frac{\mathrm{\Delta }{v}_z}{\mathrm{\Delta }t}\overrightarrow{k}$

وبالتعويض بالقيم المعطاة: ${\overrightarrow{a}}_m=\frac{(10-10)}{(1-0,5)}\overrightarrow{j}+\frac{(7,52-12,42)}{(1-0,5)}\overrightarrow{k}$

فنحصل على: ${\overrightarrow{a}}_m=-9,8\overrightarrow{k}$

استنتاج طويلة شعاع التسارع المتوسط: $a_m=\sqrt{(-9,8{)}^2}=9,8{\text{m/s}}^2$

8 ـ كتابة عبارة شعاع التسارع اللحظي:

نعبر عن التسارع اللحظي بالعبارة: $\overrightarrow{a}=\underset{\mathrm{\Delta }t\to 0}{lim}\left({\overrightarrow{a}}_m\right)$

ومنها: $\overrightarrow{a}=\underset{\mathrm{\Delta }t\to 0}{lim}\left(\frac{\mathrm{\Delta }\overrightarrow{v}}{\mathrm{\Delta }t}\right)$

ومنها: $\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$

ومنها: $\overrightarrow{a}=\frac{d{v}_x}{dt}\overrightarrow{i}+\frac{d{v}_y}{dt}\overrightarrow{j}+\frac{d{v}_z}{dt}\overrightarrow{k}$

حيث: $\frac{d{v}_x}{dt}=a_x$, $\frac{d{v}_y}{dt}=a_y$, و $\frac{d{v}_z}{dt}=a_z$

ومنها: $\overrightarrow{a}=\frac{d(0)}{dt}\overrightarrow{i}+\frac{d(10)}{dt}\overrightarrow{j}+\frac{d(-9,8t-17,32)}{dt}\overrightarrow{k}$

فنحصل على: $\overrightarrow{a}=-9,8\overrightarrow{k}$

استنتاج طويلة شعاع التسارع اللحظي: $a=\sqrt{(-9,8{)}^2}=9,8{\text{m/s}}^2$

ـ تمثيل شعاع التسارع اللحظي: (أنظر الشكل السابق)

جـ ـ عبارة التسارع الناظمي:

نعبر عن التسارع الناظمي بالعبارة التالية:

$$a_n = \frac{v^2}{r}$$

III ـ مقاربة تاريخية لميكانيك نيوتن:

1 ـ نبذة مختصرة عن أعمال غاليلي، كبلر، نيوتن:

       كان غاليلي من أتباع نظام كوبرنيك . كانت له شكوك حول المدارات الاهليلجية لكبلر . صنع منظارا بعدستين فتمكن من اكتشاف الأقمار الرئيسية للمشتري ومشاهدة النجوم ، وبمراقبة أطوار كوكب الزهراء قدم غاليلي البرهان القاطع الذي يفند كليا نظرية مركزية الأرض . فقام غاليلي سنة 1632 بنشر أشهر كتاب له (الحوار حول أكبر النظامين المسيرين للعالم)

     درس غاليلي ميكانيكية وديناميكية الأجسام في حالة الحركة وخاصة منها حركة القذائف وشرح السقوط الحر . وبين أن التسارع ثابت في حقل الجاذبية الأرضية ، فوضع قانون العطالة . كما أنه فتح النقاش حول مسألة النسبية في الحركة.

اعتمادا على أفكار كوبرنيك، ملاحظات تيكو براهي، القوانين التجريبية لكبلر وقوانين الحركة لغاليلي، طرح نيوتن نظرية على الحركات. لقد استطاع ربط القوى المطبقة  على جسم بتسارعه، كان نيوتن السباق في فهم أن التفاحة التي تسقط من شجرة والقمر الذي يدور حول الأرض يخضعان لنفس القانون فقدم قانون التجاذب الكوني. يفترض هذا القانون تزامن الفعلين المتبادلين. فاستطاع نيوتن التوحيد بين الميكانيك الأرضية والفلكية. الميكانيك الفلكية هي اذا تطبيق ميكانيك نيوتن عبر المبدأ الأساسي للتحريك ونتائجه (القوانين الثلاثة لنيوتن).

2 ـ وصف كبلر لحركة الكواكب(القوانين الثلاثة لكبلر):

القانون الأول:

تتحرك الكواكب في مدارات إهليلجيه  تكون الشمس في أحد محرقيها

نسمي b: نصف القطر الأصغري للاهليليج

نسمي a: نصف القطر الأعظمي للاهليليج

نسمي F، F': محرقي الاهليليج 

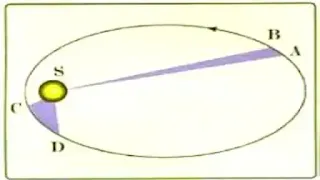
القانون الثاني:

المستقيم بين الكوكب  و الشمس يمسح مساحات متساوية خلال أزمنة متساوية

 القانون الثالث:

مربع الدور لمدار الكوكب يتناسب  طرديا  مع مكعب البعد المتوسط  للكوكب عن الشمس  ويعطى  بالعلاقة:

$$\frac{T^2}{r^3} = K$$

حيث: k : ثابت كبلر

$$K = \frac{4 \pi^2}{GM}$$

ثابت كبلر مستقل عن كتلة الكوكب

3 ـ القوانين الثلاثة لنيوتن ومفهوم التسارع:

3 ـ 1 ـ التذكير بالقانون الأول والثالث لنيوتن:

أ ـ القانون الأول:(مبدأ العطالة):

إذا كان المجموع الشعاعي للقوى المؤثرة على جسم معدوم فإن الجسم يكون ساكن أو يتحرك  بحركة مستقيمة منتظمة

$$\sum {\vec{F}}_{\text{ext}}=\vec{0}$$

ب ـ القانون الثالث: (مبدأ الأفعال المتبادلة):

 إذا أثرت جملة A على جملة B بقوة فإن الجملة B  كذلك تؤثر على الجملة A وانيا بقوة حيث

$${\vec{F}}_{A\mathrm{/}B}=-{\vec{F}}_{B\mathrm{/}A}$$

3 ـ 2 ـ القانون الثاني لنيوتن:

في معلم عطالي ، المجموع الشعاعي للقوى الخارجية المطبقة على جملة  ميكانيكية  يساوي في كل لحظة جداء كتلتها  في  شعاع  تسارع  مركز عطالتها:

$$\sum {\vec{F}}_{\text{ext}}=m{\vec{a}}_G$$

IV ـ تطبيقات قوانين نيوتن:

1 ـ حركة الكواكب و الأقمار الاصطناعية:

نشاط ـ 1 ـ

ليكن لدينا كوكب يدور حول الشمس أو قمر يدور حول الأرض كما يوضحه الشكل التالي:

ـ أذكر أهم خصائص الحركة الدائرية المنتظمة ؟

ـ مسار دائري

ـ السرعة ثابتة الشدة

ـ يخضع الجسم خلال حركته لقوة شدتها ثابتة وجهتها نحو مركز المسار الدائري 

ـ عرف دور الحركة الدائرية المنتظمة  T وأكتب عبارته بدلالة نصف القطر r والسرعة v ؟

الدور هو الزمن اللازم لإنجاز دورة واحدة ونرمز له بالرمز T ويعطى بالعبارة  T = 2πr/v

ـ بالاعتماد على عبارتي التسارع الناظمي $a_n$ والدور $T$بين أن:

$$a_n = \frac{4\pi^2 r}{T^2}$$

لدينا:

$$a_n = \frac{v^2}{r} \quad \rightarrow (1)$$

ولدينا:

$$T = \frac{2\pi r}{v}$$

ومنه:

$$v = \frac{2\pi r}{T}$$

بتربيع الطرفين نجد:

$$v^2 = \frac{4\pi^2 r^2}{T^2} \quad \rightarrow (2)$$

بتعويض (2) في (1) نجد:

$$a_n = \frac{\frac{4\pi^2 r^2}{T^2}}{r}$$

ومنه:

$$a_n = \frac{4\pi^2 r}{T^2}$$

ـ بالاعتماد على القانون الثاني لنيوتن أوجد عبارة القوة الناظمية F_n ؟

بتطبيق القانون الثاني لنيوتن

$$\sum \vec{F}_{\text{ext}} = m \vec{a}_G$$

نجد:

$${\vec{F}}_n=m{\vec{a}}_n$$

بالإسقاط على المحور الناظمي  نجد:  F_n = m.a_n

ـ أكتب عبارة قوة الجذب العام  F_g بالاعتماد على قانون الجذب العام ؟

لدينا:

$$F_g=G\frac{mM}{r^2}$$

ـ من العلاقتين السابقتين بين أن 

$$v=\sqrt{\frac{GM}{r}}$$

لدينا:

$$F_n = m a_n$$

ولدينا:

$$a_n = \frac{v^2}{r}$$

ومنه:

$$F_n = m \frac{v^2}{r}$$

ولدينا:

$$F_n = F_g$$

ومنه:

$$m \frac{v^2}{r} = G \frac{m M}{r^2}$$

ومنه:

$$\frac{v^2}{r} = G \frac{M}{r^2}$$

ومنه:

$$v^2 = \frac{G M}{r}$$

ومنه:

$$v = \sqrt{\frac{G M}{r}} \quad \rightarrow (3)$$

تعبر العلاقة (3) عن السرعة المدارية ومنه نكتب:

$$v_{\text{orb}} = \sqrt{\frac{G M}{r}}$$

 ـ استنتج عبارة السرعة المدارية لكوكب يدور حول الشمس إذا كانت كتلة الشمس هي M_s ؟

$$v_{\text{orb}}=\sqrt{\frac{G{M}_s}{r}}$$

حيث:

 M_s: كتلة الشمس

r: البعد بين مركز الكوكب ومركز الشمس

ـ استنتج  عبارة الدور لكوكب يدور حول الشمس ؟

لدينا:

$$T = \frac{2\pi r}{v}$$

ولدينا:

$$v = \sqrt{\frac{GM}{r}}$$

ومنه:

$$T = 2\pi r \sqrt{\frac{r}{GM}}$$

ومنه:

$$T = 2\pi \sqrt{\frac{r^3}{GM}}$$

في حالة كوكب يدور حول الشمس نجد:

$$T = 2\pi \sqrt{\frac{r^3}{G M_s}}$$

ـ استنتج  عبارة السرعة المدارية لقمر يدور حول الأرض إذا كانت كتلة الأرض هي  M_T ؟

$$v_{\text{orb}}=\sqrt{\frac{G{M}_T}{R+h}}$$

حيث :

 M_T : كتلة الأرض 

  R : نصف قطر الأرض 

 h : البعد بين مركز القمر وسطح الأرض 

 ـ استنتج  عبارة الدور لقمر يدور حول الأرض ؟

$$T=2\pi \sqrt{\frac{(R+h{)}^3}{G{M}_s}}$$

2 ـ حركة مركز عطالة جسم صلب خاضع لعدة قوى:

أ ـ التذكير بأنواع الحركات المستقيمة ومعادلاتها الزمنية:

الحركة المستقيمة المنتظمة
المسار	مستقيم
السرعة	ثابتة
التسارع	معدوم
معادلات تفاضلية	$\frac{dv}{dt}=0$ لأن $v=\text{Cte}$ $\frac{dx}{dt}=v=\text{Cte}\ne 0$
المعادلات الزمنية	x = v.t + x0

الحركة المستقيمة المتغيرة بانتظام
المسار	مستقيم
السرعة	متغيرة بانتظام
التسارع	ثابت
معادلات تفاضلية	$\frac{dv}{dt}=a=\text{Cte}\ne 0$ $\frac{dx}{dt}=v$ $\frac{dx}{dt}=a\cdot t+v_0$
المعادلات الزمنية	$v=a\cdot t+v_0$ $x=\frac{1}{2}a{t}^2+v_{0}t+x_0$

ايجاد العلاقة الشهيرة:

لدينا: $v=a\cdot t+v_0$

ومنه: $t=\frac{v-v_0}{a}\text{(1)}$

ولدينا: $x=\frac{1}{2}a{t}^2+v_{0}t+x_0$

ومنه: $x-x_0=\frac{1}{2}a{t}^2+v_{0}t\text{(2)}$

بتعويض (1) في (2) نجد: $x-x_0=\frac{1}{2}a{\left(\frac{v-v_0}{a}\right)}^2+v_0\left(\frac{v-v_0}{a}\right)$

ومنه: $x-x_0=\frac{v-v_0}{a}[\frac{1}{2}(v-v_0)+v_0]$

ومنه: $x-x_0=\frac{v-v_0}{2a}(v+v_0)$

ومنه: $x-x_0=\frac{1}{2a}(v^2-v_0^2)$

ومنه: $v^2-v_0^2=2a(x-x_0)$

ب ـ دراسة الحركة على المستوي الافقي:

نشاط ـ 1 ـ

      لتكن الجملة الميكانيكية الموضحة بالشكل التالي :حيث أن البكرة مهملة الكتلة والخيط مهمل الكتلة و عديم الامتطاط.

نفرض أن الجملة تنطلق من السكون

1 ـ حدد جهة الحركة ؟

أنظر التمثيل المرفق

 2 ـ مثل القوى المؤثرة على كل جسم ؟

أنظر التمثيل السابق

3 ـ بتطبيق القانون الثاني لنيوتن ، حدد طبيعة حركة الجملة ؟

بتطبيق القانون الثاني لنيوتن على كل جسم على حدا والإسقاط على اتجاه الحركة

الجسم 1 :  نجد:

$${\vec{P}}_1+{\vec{T}}_1=m_1\vec{a}$$

ومنه 

P₁ – T₁ = m₁.a → (1)

   الجسم 2 :  نجد:

$${\vec{P}}_2+{\vec{T}}_2+{\vec{R}}_2=m_2\vec{a}$$

ومنه

T₂ = m₂.a → (2)

   بما أن البكرة مهملة الكتلة فإن التوترين على طرفيها متساويين T₁ = T₂

    بجمع (1) و (2) طرف إلى طرف نجد :  P₁ = (m₁ +m₂).a  حيث  P = m.g

  ومنه نجد:

$$a=\frac{m_{1}g}{m_1+m_2}=\text{Cte}$$

 بما أن التسارع مقدار ثابت موجب فإن الحركة مستقيمة متسارعة بانتظام

4 ـ أوجد معادلاتها الزمنية ؟

معادلة السرعة: v(t) = a.t

معادلة الفاصلة: x(t) =½.at²

جـ ـ دراسة الحركة على المستوي المائل:

نشاط ـ 2 ـ

     نترك جسم صلب (S) كتلته m ينزلق على مستوي مائل كما يوضحه الشكل التالي:

     بتطبيق القانون الثاني لنيوتن - أوجد عبارتي تسارع مركز عطالة الجسم وكذا رد فعل المستوي وذلك في حالة وجود قوى احتكاك وفي حالة عدم وجودها ؟ 

ايجاد عبارة تسارع الجسم في حالة وجود قوى احتكاك:

تمثيل القوى المؤثرة على الجسم وتحديد جهة الحركة

 بتطبيق القانون الثاني لنيوتن

$$\sum {\vec{F}}_{\text{ext}}=m{\vec{a}}_G$$

 نجد:

$$\vec{P}+\vec{R}+\vec{f}=m\vec{a}$$

بالإسقاط على المحور $(X' X)$ نجد:

$$P_x - f = ma$$

ولدينا:

$$\sin \alpha = \frac{P_x}{P}$$

ومنه:

$$P_x = P \sin \alpha$$

ولدينا:

$$P = mg$$

ومنه:

$$P_x = mg \sin \alpha$$

ومنه:

$$mg \sin \alpha - f = ma$$

ومنه:

$$a = g \sin \alpha - \frac{f}{m}$$

ايجاد عبارة تسارع الجسم في حالة عدم وجود قوى احتكاك:

نضع f = 0  ومنه نجد: a = g.sinα

ايجاد عبارة قوة رد الفعل:

بالإسقاط على المحور $(Y' Y)$ نجد:

$$-P_y + R = 0$$

ومنه:

$$R = P_y$$

ولدينا:

$$\cos \alpha = \frac{P_y}{P}$$

ومنه:

$$P_y = P \cos \alpha$$

ومنه:

$$P_y = mg \cos \alpha$$

ومنه:

$$R = mg \cos \alpha$$

وثيقة التلميذ بصيغة الـ PDF