الطاقة الكامنة. الاجابة عن أهم الأسئلة

في هذا الدرس، نناقش الطاقة الكامنة، وهي نوع من الطاقة التي تمتلكها الأجسام بسبب موقعها أو تكوينها. ما هي الطاقة الكامنة؟ هي الطاقة المخزنة في جسم أو نظام نتيجة لوضعه أو حالته. يمكن أن تكون الطاقة الكامنة الجاذبية، حيث تعتمد على ارتفاع الجسم عن سطح الأرض، أو الطاقة الكامنة المرنة، الناتجة عن تمدد أو انضغاط الأجسام مثل النابض.

1 ـ الطاقة الكامنة الثقالية:

1 ـ 1 ـ الجملة المتماسكة:

ـ عرف الجملة المتماسكة ؟

الجملة المادية المتماسكة، هي جملة تبقى ﺍﻷﺒﻌﺎﺩ ﺒﻴﻥ ﺍﻟﻨﻘﺎﻁ ﺍﻟﻤﺅﻟﻔﺔ ﻟﻬا ﺜﺎﺒﺘﺔ ﺃﺜﻨﺎﺀ الحركة

1 ـ 2 ـ الجملة الغير متماسكة (القابلة للتشوه):

ـ عرف الجملة المادية الغير المتماسكة ؟

ﺍﻟﺠﻤﻠﺔ ﺍﻟﻤﺎﺩﻴﺔ الغير متماسكة، هي جملة تتغير ﺍﻷﺒﻌﺎﺩ ﺒﻴﻥ ﺍﻟﻨﻘﺎﻁ ﺍﻟﻤﺅﻟﻔﺔ ﻟﻬا ﺃﺜﻨﺎﺀ الحركة أو عند التأثير عليها بمؤثر خارجي ، أي جملة قابلة للتشوه

1 ـ 3 ـ الطاقة الكامنة الثقالية لجسم في تأثير متبادل مع الأرض:

1 ـ 3 ـ 1 ـ مدلول الطاقة الكامنة الثقالية:

نترك جسما يسقط من النقطة A نحو النقطة B من سطح الأرض حيث AB = z   فكلما  كانتA  أبعد عنB  كلما كانت الطاقة الحركية للجسم أكبر عند وصوله إلىB  . هذه الطاقة الحركية لم تكن سوى طاقة مخزنة  فيه تسمى الطاقة الكامنة الثقالية.

1 ـ 3 ـ 2 ـ عبارة الطاقة الكامنة الثقالية:

عند انتقال جسم من الموضع A نحو الموضع B  بسرعة ثابتة أي  V_A = V_B  فإنه عند الصعود و بتطبيق مبدأ انحفاظ الطاقة نجد:

$$E_{C_A} + W_{AB}(\vec{F}) - |W_{AB}(\vec{P})| = E_{C_B}$$

وبما أن:

$$v_A = v_B$$

نستنتج:

$$W_{AB}(\vec{F}) = -W_{AB}(\vec{P})$$

وبالتعويض:

$$W_{AB}(\vec{F}) = -(-m \cdot g \cdot (z_B - z_A))$$

ونحصل على:

$$W_{AB}(\vec{F})=m\cdot g\cdot z_B-m\cdot g\cdot z_A$$

نسمي:

• $m \cdot g \cdot z_A$ الطاقة الكامنة الثقالية للجسم عند النقطة $A$.
• $m \cdot g \cdot z_B$ الطاقة الكامنة الثقالية للجسم عند النقطة $B$.

ونكتب المعادلة:

$$W_{AB}(\vec{F}) = E_{\text{pp}_B} - E_{\text{pp}_A}$$

ومنه:

$$W_{AB}(\vec{F})=\mathrm{\Delta }{E}_{\text{pp}}$$

ومنه:

$$W_{AB}(\vec{P})=-\mathrm{\Delta }{E}_{\text{pp}}$$

نتيجة:    

كل جسم كتلتهm  موجود على ارتفاع h عن سطح الأرض يملك طاقة كامنة ثقالية : E_pp = mgh

    حيث:, m(kg) , g( N/kg) , h(m)   E_pp(J)

ملاحظة:

الطاقة الكامنة الثقالية  تتعلق بالارتفاع h  وهذا الأخير يحدد في مرجع مختار نعتبر عنده الارتفاع يساوي الصفر نسميه المستوى المرجعي للطاقة الكامنة الثقالية ومنه الطاقة الكامنة الثقالية تتعلق بالمرجع المختار أي معرفة بتقريب ثابت.

2 ـ الطاقة الكامنة المرونية:

نشاط ـ 1 ـ مقاربة أولية لعبارة الطاقة الكامنة المرونية:

نربط جسما كتلته  m الى أحد طرفي نابض طويل ثم نتركه يسقط من الموضع A (الشكل 3 ب) دون سرعة ابتدائية فيستطيل النابض حتى الموضع  B أين تنعدم سرعة الجسم ويستطيل النابض بالمقدار x (الشكل 3 ج)

توضيح: الموضع  B كيفي تحدده الاستطالة x

1 ـ بتطبيق مبدأ انحفاظ الطاقة بين الموضعين A و B

ـ بين أن : E_pe = - ΔE_pp حيث E_pe هي الطاقة الكامنة المرونية للنابض ؟

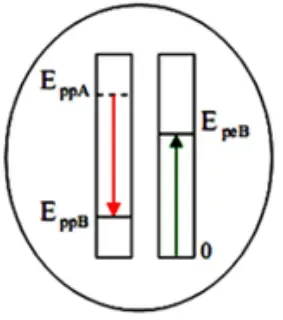
لدينا: الحصيلة الطاقوية للجملة (جسم + نابض)

معادلة انحفاظ الطاقة تكتب على الشكل:

E_ppA + E_peA = E_ppB + E_peB  حيثE_peA = 0  

 ومنه:  E_peB = E_ppA + E_ppB ، وبالتالي E_peB = - ΔE_pp

2 ـ نكرر التجربة من أجل قيم مختلفة للكتلة m ونقيس في كل مرة استطالة النابض.

ومنه تم الحصول على النتائج التالية:

x2(m2)	mgx(J)	x(m)	m(Kg)
2,4×10-3	0,048	0,049	0,1
9,6×10-3	0,192	0,098	0,2
3,8×10-2	0,768	0,196	0,4
6,0×10-2	1,200	0,245	0,5

 ـ أرسم المنحنى الممثل لتغيرات E_pe بدلالة المقدار x² ؟

لدينا: ΔE_pp = E_ppB – E_ppA = mgh – mg(h + x)

ومنه: ΔE_pp = - mgx

لدينا من جهة أخرى: E_peB = - ΔE_pp = - (- mgx) = mgx

ملاحظة: المستوي المرجعي  لقياس E_pp أسفل الموضع B

ـ ماذا تلاحظ ؟

نلاحظ أن البيان عبارة عن خط مستقيم يمر امتداده من المبدأ

3 ـ أحسب معامل توجيه المنحنى واستنتج أن عبارة الطاقة الكامنة المرونية تكتب على الشكل : E_pe = K_e.x² ؟

معامل توجيه البيان هو:

$$\frac{FG}{EG}=20\text{SI}$$

المنحنى البياني عبارة عن خط مستقيم يمر من المبدأ معادلته هي: E_pe = K_e.x²

حيث: K_e = 20 SI هو معامل توجيه البيان

نشاط ـ 2 ـ تعيين الثابت K_e:

  لتعيين الثابت K_e نقوم بمعايرة النابض المستعمل في التجربة السابقة.

نعلق في نهاية النابض أجساما مختلفة الكتل ونقيس في كل مرة الاستطالة عند وضعية توازن الجسم

0,7	0,6	0,4	0,3	m(Kg)
6,86	5,88	3,92	2,94	mg =T(N)
17,1	14,7	9,8	7,3	ΔL = x(cm)

1 ـ مثل القوى المطبقة على الجملة عند التوازن ؟

تمثيل القوى:

عند التوازن نجد: T = P = m.g

2 ـ أرسم منحنى المعايرة الممثل لتغيرات شدة القوة المطبقة على النابض بدلالة الاستطالة ؟

3 ـ أحسب معامل توجيه المنحنى الذي يمثل ثابت مرونة النابض ؟

معامل توجيه المنحنى هو ثابت مرونة النابض K لأن قوة التوتر تكتب بالشكل T = K.x

لدينا:

$$K=\frac{HJ}{IJ}=40\text{SI}$$

4 ـ قارن قيمة معامل التوجيه مع قيمة K_e . ماذا تلاحظ ؟

بتكرار التجربة بنوابض مختلفة نلاحظ أن : Ke = ½.K في حدود أخطاء التجربة

وبالتالي عبارة الطاقة الكامنة المرونية تكتب بالشكل : E_pe = ½Kx²

حيث وحدة ثابت مرونة النابض هي (N/m)

نتيجة: عندما يستطيل أو ينضغط  نابض ثابت مرونته K بمقدار x ، تكتب عبارة الطاقة الكامنة المرونية بالشكل:

E_pe = ½Kx²

3 ـ الطاقة الكامنة المرونية لنواس فتل:

نشاط ـ 1 ـ معايرة نابض الفتل:

نثبت نابض حلزوني مسطح ندعوه نابض فتل (1) من طرفه الداخلي في النقطة O، كما هو مبين في الشكل التالي:

باستعمال نابض (2) معاير ثابت مرونته K ، طبق على الطرف الحر لنابض الفتل (1) قوة عمودية على AO.

اختر مرجعا لقياس زاوية دوران نقطة تطبيق القوة.

1 ـ غير في شدة القوة المطبقة وقس في كل مرة استطالة النابض (2) وزاوية دوران نابض الفتل (1) ؟

2 ـ دون نتائجك في الجدول التالي ؟

النتائج:

عزم القوة بالنسبة الى نقطة تثبيت نابض الفتل	شدة القوة F(N)	زاوية دوران نابض الفتل θ(rd)	استطالة النابض (2) x(cm)
0,2058	2,94	1,04	7,3
0,2744	3,92	1,40	9,8
0,4116	5,88	2,10	14,7

3 ـ أرسم تغيرات عزم القوة بدلالة تغيرات زاوية دوران نابض الفتل ؟

4 ـ أحسب ميل المنحنى الذي يمثل ثابت فتل النابض ؟

لدينا:

$$C=\frac{BD}{AD}=\frac{2.8\times 0.05}{1.5\times 0.5}$$

ومنه:

$$C=\frac{0.14}{0.75}=0.1867$$

ومنه:

$$C=0.1867$$

نشاط ـ 2 ـ الطاقة الكامنة المرونية لنواس الفتل:

لحساب الطاقة المخزنة في نابض الفتل المستعمل في النشاط ـ 1 ـ نقبل ان الطاقة المخزنة في نابض الفتل (1) تساوي في كل وضعية الطاقة المخزنة في النابض (2) . يمكن الوصول الى هذه النتيجة بتوظيف مبدأ انحفاظ الطاقة ومبدأ الفعلين المتبادلين وذلك بدراسة الجملتين النابض(1) والنابض(2).

باستعمال نتائج النشاط  ـ 1 ـ املأ الجدول التالي:

θ2(rd2)	الطاقة المخزنة في النابض (1) ½Kx2 (J)	زاوية دوران نابض الفتل θ(rd)	استطالة النابض (2) x(cm)
1.0874	0,1066	1,04	7,3
1.9600	0,1921	1,40	9,8
4.4100	0,4322	2,10	14,7

1 ـ أرسم منحنى تغيرات الطاقة المخزنة في النابض (1) بدلالة مربع الزاوية θ² ؟

2 ـ أحسب ميل المنحنى واستنتج أن عبارة الطاقة الكامنة المرونية لنابض الفتل تكتب على الشكل: 

E_pt = C_e.θ² ؟

لدينا:

$$C_e=\frac{MN}{LN}=\frac{4.8\times 0.05}{2.5\times 1}$$

ومنه:

$$C_e=\frac{0.24}{2.5}=0.096\text{SI}$$

ومنه:

$$C_e = 0.096 \, \text{SI}$$

3 ـ قارن قيمة C_e مع قيمة ثابت فتل النابض C. ماذا تلاحظ ؟

لدينا:

$$\frac{C}{C_e}=\frac{0.187}{0.096}\approx 2$$

ومنه نلاحظ أن: C_e = ½C

4 ـ استنتج أن عبارة الطاقة الكامنة المرونية لنابض الفتل تكتب على الشكل: E_pt = …Cθ² ؟

لدينا: E_pt = C_e.θ² ولدينا: C_e = ½C  ومنه: E_pt = ½.C.θ²

نتيجة:

عندما نفتل بزاوية θ سلك فتل أو نابض حلزوني (نابض الفتل)ثابت فتله C، فانه يخزن طاقة كامنة مرونية عبارتها 

 E_pt = ½Cθ²