مقاربات الأفعال المتبادلة الكهرومغناطيسية. الاجابة عن أهم الأسئلة

تشير مقاربات الأفعال المتبادلة الكهرومغناطيسية إلى التفاعلات الفيزيائية، التي تحدث بين المجالات الكهربائية والمغناطيسية، والتي تُعرف علميًا باسم القوى الكهرومغناطيسية. هذه القوى هي إحدى القوى الأساسية في الطبيعة، وتُفسَّر من خلال قانون ماكسويل، حيث تربط بين الكهرباء والمغناطيسية في إطار واحد. تظهر هذه الأفعال في الحياة اليومية من خلال ظواهر مثل التيارات الكهربائية، الحقول المغناطيسية، والموجات الكهرومغناطيسية مثل الضوء.

تُعد هذه المقاربات أساسًا للعديد من التطبيقات التكنولوجية، مثل الاتصالات اللاسلكية، أنظمة الطاقة الكهربائية، وتقنيات الاستشعار.

ملاحظة: توجد وثيقة التلميذ بصيغة الـ PDF في نهاية المقال.

1 ـ تجارب حول الافعال المتبادلة الكهرومغناطيسية:

1 ـ 1 ـ اثبات وجود قوة كهرومغناطيسية:

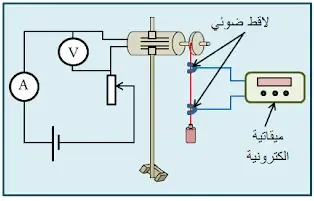
نحقق تركيب الدارة الكهربائية المبينة بالشكل المقابل.

ـ نغلق القاطعة . هل ينحرف السلك؟

السلك لا ينحرف لأنه غير مغمور في حقل مغناطيسي.

ـ نفتح القاطعة ونضع السلك بين فكي مغناطيس ، ماذا تشاهد؟

لا شيء.

ـ نغلق القاطعة. هل ينحرف السلك ؟

نلاحظ انحراف السلك. حيث ينحرف الى يمين أو يسار، (الشكل السابق)، حسب وضع أقطاب المغناطيس.

ـ نفتح القاطعة، ونقلب قطبي المغناطيس ثم نغلقها. ماذا يحدث؟

نلاحظ انحراف السلك نحو الجهة المعاكسة.

ـ نفتح القاطعة، ونعكس توصيل قطبي البطارية ثم نغلق. ماذا يحدث؟

نلاحظ انحراف السلك نحو الجهة المعاكسة.

نتيجة:

عندما يمر تيار كهربائي في ناقل مغمور في حقل مغناطيسي، فانه يخضع لقوة كهرومغناطيسية. تتعلق جهة القوة الكهرومغناطيسية المؤثرة على السلك بجهة الحقل المغناطيسي، وجهة مرور التيار الكهربائي فيه.

1 ـ 2 ـ علاقة القوة الكهرومغناطيسية بشدتي الحقل المغناطيسي، والتيار الكهربائي المار في الدارة:

ـ غير قيمة مقاومة المعدلة حتى تتغير شدة التيار ثم أغلق القاطعة. ماذا تلاحظ ؟

نلاحظ انتقال القضيب.

ـ اضبط شدة التيار عند قيمة معينة، واستبدل المغناطيس باخر أقوى منه. ماذا تلاحظ ؟

نلاحظ انتقال القضيب بسرعة أكبر.

نتيجة:

تتعلق شدة القوة الكهرومغناطيسية المؤثرة على القضيب بشدة التيار الكهربائي المار به، وشدة الحقل المغناطيسي المغمور فيه.

1 ـ 3 ـ تجربة السكتين (دراسة خصائص قوة لابلاص):

نحقق التجربة المبينة في الشكل التالي:

ـ اقترح خطوات عملية لتبرير كل من جهة وشدة الحقل المغناطيسي، وجهة وشدة التيار الكهربائي في السلك؟

معرفة جهة الحقل المغناطيسي بتقريب ابرة مغناطيسية من اقطاب المغناطيس. أما شدته عن طريق توفير مغانط مختلفة بعضها ضعيفة الحقل المغناطيسي، وأخرى أقوى.

معرفة جهة التيار الكهربائي من خلال أقطاب المولد المستعمل في الدارة الكهربائية. أما شدته عن طريق توصيل أمبير متر على التسلسل في الدارة الكهربائية، وتغيير شدة التيار الكهربائي يتم بواسطة معدلة توصل على التسلسل في الدارة الكهربائية.

ـ كيف يكون وضع هذه القوة بالنسبة لشعاع الحقل، وشدة التيار؟

يحدد وضع هذه القوة بالنسبة لشعاع الحقل، وشدة التيار بتطبيق قاعدة اليد اليمنى:

* قاعدة اليد اليمنى.

ـ أستنتج علاقة رياضية تربط القوة الناشئة بالمقداير المؤثرة فيها ؟

الاجابة:

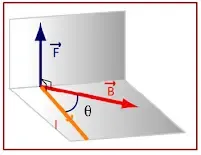
يوجد تناسب طردي بين شدة القوة الكهرومغناطيسية F، وكل من شدة التيار الكهربائي I، وشدة شعاع الحقل المغناطيسي B، وطول الجزء من الناقل المغمور في الحقل المغناطيسي l. دون أن ننسى تأثير الزاوية θ بين الناقل ومحصلة شعاع الحقل المغناطيسي .حيث تتحقق العلاقة التالية: F = I.l.B.sin θ

نتيجة:

للقوة الكهرومغناطيسية حامل عمودي على القضيب، وعلى شعاع الحقل المغناطيسي المطبق على القضيب، أي عمودي على المستوي الذي يحتوي القضيب، وحامل شعاع الحقل المغناطيسي.

تتعلق قيمة (شدة) القوة الكهرومغناطيسية المؤثرة على القضيب بطول الجزء المغمور من القضيب في الحقل المغناطيسي، وشدة التيار الكهربائي الذي يمر فيه.

1 ـ 4 ـ ميزان كوطون أو تجربة الاطار لقياس شدة حقل مغناطيسي:

أ ـ ميزان كوطون:

لقياس الحقول المغناطيسية نستعمل التسلامتر الذي يعتمد على ظاهرة هول، ولكن قبل ابتكاره استعمل ميزان كوطون.

نعطي في الشكل مبدأ تركيب هذا الميزان، الذي يحتوي من جهة كفة ميزان عادية، ومن جهة أخرى صفيحة عازلة (S)، يلتصق في أطرافها ADCE شريط ناقل يعبره تيار I، ويغمر في الحقل المغناطيسي الذي نريد قياسه، الطرفان AD وCE جزءان من دائرتين لهما نفس المركزO، والطرف CD مستقيم الشكل.

عندما نغمر جزءا من الصفيحة (S) في حقل مغناطيسي منتظم، شعاعه عمودي على مستوى الشكل، يختل التوازن عندما نمرر تيارا كهربائيا في الناقل.

* نضع كتلا عيارية في الكفة من أجل إعادة التوازن.

* نغير من شدة التيارI المار في الدارة باستخدام المعدلة.

ونعيد توازن الميزان باستخدام كتل عيارية m، ونسجل النتائج في الجدول التالي:

					I(A)
					m(g)

1 ـ أرسم المنحنى البياني m = f(I)، ماذا تستنتج ؟

2 ـ اعتمادا على البيان استنتج شدة الحقل المغناطيسي B في هذه التجربة علما أن:

 g = 10 N/Kg  , CD = L = 2cm  , d = d'

الاجابة:

1 ـ جدول القياسات:

10	8	6	4	2	I(A)
10	8	6	4	2	m(g)

 رسم المنحنى البياني  m = f(I)

الاستنتاج:

المنحنى عبارة عن خط مستقيم يشمل المبدأ معادلته من الشكل

  m = a . I ……(1)

حيث a يمثل ميل المستقيم

نستنتج ان m تتناسب طرديا مع I

2 ـ استنتاج شدة الحقل المغناطيسي B عند التوازن:

لدينا:

$$M_{(\vec{F} \,/\, \Delta)} + M_{(\vec{P} \,/\, \Delta)} + M_{(\vec{R} \,/\, \Delta)} = 0$$

ومنه:

$$F \cdot d' - P \cdot d = 0$$

وبما أن:

$$d = d' \Rightarrow F = P$$

ومنه:

$$B \cdot I \cdot L = m \cdot g \Rightarrow B = \frac{m \cdot g}{I \cdot L}$$

لحساب $\frac{m}{I}$:
من البيان نجد:

$$a = \frac{m}{I} = \frac{m_2 - m_1}{I_2 - I_1}$$

وبالتعويض:

$$a = \frac{(10 - 2) \times 10^{-3}}{10 - 2} = \frac{8 \times 10^{-3}}{8} = 10^{-3}$$

ومنه:

$$B = \frac{a \cdot g}{L}$$

وبالتعويض:

$$B=\frac{{10}^{-3}\cdot 10}{2\times {10}^{-2}}=\frac{{10}^{-2}}{2\times {10}^{-2}}=0.5\text{ T}$$

ب ـ الاطار المتحرك:

نحقق التركيب التجريبي التالي:

عند مرور التيار الكهربائي في الاطار، وهو مغمور في حقل مغناطيسي منتظم يبدأ الاطار بالدوران حول المحور (Δ).

1 ـ مثل على الرسم كل من شعاع الحقل المغناطيسي، والقوى المؤثرة على أضلاع الاطار؟

تمثيل شعاع الحقل المغناطيسي، والقوى المؤثرة على أضلاع الاطار.

2 ـ ما هو أثر القوى المؤثرة على الاطار؟

نلاحظ أن القوتان

$${\vec{F}}_1,{\vec{F}}_3$$

 متساويتان في الشدة، ومتعاكستان في الجهة، ولهما نفس الحامل، ومنه فان الأثر الاجمالي للقوتين على الاطار معدوم. 

أما القوتان

$${\vec{F}}_2,{\vec{F}}_4$$

فهما متساويتان في الشدة، ومتعاكستان في الجهة، و حاملاهما متوازيان، ومنه تنشأ مزدوجة قوتين تؤدي الى دوران الاطار حول المحور (Δ).

3 ـ أوجد عبارة عزم المزدوجة ؟

الاجابة:

لدينا: F₂ = F₄ = F = B.I.a

ولدينا: M_/Δ = F.d  حيث: d = b.sinθ ومنه: M_/Δ = F.b.sinθ

بتعويض عبارة F نجد: M_/Δ = B.I.a.b.sinθ

ولدينا: a.b = S   ومنه: M_/Δ = B.I.S.sinθ

2 ـ تطبيقات حول قانون لابلاص:

3 ـ الربط الكهروميكانيكي:

3 ـ 1 ـ الدراسة التجريبية لمكبر الصوت:

تتأثر الوشيعة المثبتة على غشاء ورقي مرن، الموجود في الفراغ البيني لمغناطيس مكبر الصوت، عندما يعبرها تيار كهربائي بقوة كهرومغناطيسية موازية لمحورها، وتتبع تغيراتها تغيرات شدة التيار المار في الوشيعة، محدثة حركة اهتزازية للغشاء منتجة أمواجا صوتية في الهواء. مكبر الصوت هو عبارة عن محول كهروميكانيكي، يحول الطاقة الكهربائية التي يتلقاها الى طاقة ميكانيكية، تظهر في حركة الغشاء.  

3 ـ 2 ـ تحديد المردود الطاقوي لمحرك كهربائي:

نحقق التركيب التجريبي التالي:

ترتفع الحمولة مسافة h = 1m، نقيس الزمن اللازم لقطع هذه المسافة نحصل على الجدول التالي:

h (m)	M(Kg)	t (s)	I (A)	U(v)
1,0	0,10	1,1	0,25	4,8
1,0	0,15	1,3	0,30	4,8
1,0	0,20	1,5	0,37	4,5
1,0	0,25	1,9	0,37	4,6

1 ـ اعتمادا على هذا التركيب صف باختصار مبدأ التجربة موضحا دور كل عنصر؟

2 ـ هل يمكن اعتبار أن سرعة الحمولة ثابتة خلال مدة القياس؟

3 ـ أحسب سرعة الحمولات في هذه القياسات؟

4 ـ أحسب الطاقة الحركية لمختلف الحمولات عندما تصل الى علو 1,5 m ؟

5 ـ أعط العبارة الحرفية للاستطاعة الكهربائية المقدمة من طرف المحرك في كل حالة ؟

6 ـ أعط عبارة عمل ثقل الحمولة خلال الصعود بين المستويين 0,50 m و 1,50 m ؟

7 ـ أستنتج عبارة الاستطاعة الميكانيكية المقدمة للحمولة من طرف المحرك ؟

8 ـ أعط العبارة الحرفية لمردود المحرك η، علما أن مردود المحرك هو النسبة بين الاستطاعة الميكانيكية المبذولة من طرف المحرك، والاستطاعة الكهربائية المقدمة للمحرك، أي:  η = P_m/P_e

9 ـ أكمل الجدول التالي: 

المردود	الاستطاعة الميكانيكية Pm	الاستطاعة الكهربائية Pe	الحمولة M (Kg)
			0,10
			0,15
			0,20
			0,25

الاجابة:

1 ـ توضيح دور كل عنصر:

المولد: توليد التيار الكهربائي.

الأمبيرمتر: قياس شدة التيار.

الفولطمتر: قياس شدة التوتر بين طرفي المحرك.

المحرك الكهربائي: تحويل الطاقة الكهربائية إلى ميكانيكية لرفع الحمولة.

الميقاتية: قياس الزمن اللازم لرفع الحمولة مسافة h.

2 ـ نعم يمكن اعتبار أن سرعة الحمولة ثابتة خلال مدة القياس.

3 ـ حساب سرعة الحمولات في هذه القياسات:

لدينا: v = h/t

v(m/s)	h (m)	t (s)
0,91	1,0	1,1
0,77	1,0	1,3
0,67	1,0	1,5
0,53	1,0	1,9

مما سبق نستنتج  أن سرعة الحمولة ليست ثابتة خلال مدة القياس.

4 ـ حساب الطاقة الحركية لمختلف الحمولات عندما تصل الى علو 1,5 m:

0,53	0,67	0,77	0,91	v(m/s)
0,0351	0,0448	0,0444	0,0414	EC(J)

5 ـ اعطاء العبارة الحرفية للاستطاعة الكهربائية المقدمة من طرف المحرك في كل حالة:

لدينا: P_e = U.I

6 ـ اعطاء عبارة عمل ثقل الحمولة خلال الصعود بين المستويين 0,50m و 1,50m :

لدينا: W_m = M.g.h

7 ـ استنتاج عبارة الاستطاعة الميكانيكية المقدمة للحمولة من طرف المحرك:

لدينا:

$$P_m = \frac{W_m}{t} = \frac{Mgh}{t}$$

ولدينا:

$$\frac{h}{t} = v$$

ومنه:

$$P_m=Mgv$$

8 ـ اعطاء العبارة الحرفية لمردود المحرك η:

لدينا:

$$\eta = \frac{P_m}{P_e}$$

حيث:

$$P_e = U \cdot I \quad \text{و} \quad P_m = Mgv$$

وبالتعويض:

$$\eta =\frac{Mgv}{U\cdot I}$$

9 ـ اتمام الجدول:

المردود	الاستطاعة الميكانيكية Pm	الاستطاعة الكهربائية Pe	الحمولة M (Kg)
74,42 %	0,893	1,2	0,10
78,68 %	1,133	1,44	0,15
79,15 %	1,314	1,66	0,20
76,47 %	1,300	1,70	0,25

اقرأ حلول تمارين مقاربات الافعال المتبادلة الكهرومغناطيسية

وثيقة التلميذ بصيغة الـ PDF