القوة والحركات المستقيمة. الاجابة عن أهم الأسئلة

تُعتبر القوة والحركات المستقيمة، من الأسس الرئيسية في علم الميكانيك الكلاسيكي، و تُركز على دراسة العلاقة بين القوة المؤثرة على جسم، وحركته في خط مستقيم. يتم وصف الحركة المستقيمة من خلال قوانين نيوتن للحركة، التي تُحدد كيفية تأثير القوى على الأجسام لتغيير سرعتها، أو اتجاهها.

ملاحظات:

1/ توجد وثيقة التلميذ بصيغة الـ PDF في نهاية المقال.

2/ توجد البطاقـة التربويـة لدرس القوة والحركات المستقيمة بصيغة الـ PDF في نهاية المقال (نموذج عادي).

3/ توجد البطاقـة التربويـة لدرس القوة والحركات المستقيمة بصيغة الـ PDF في نهاية المقال (نموذج مخصص).

I ـ دراسة نص (ظهور التصور الميكانيكي):

الوثيقة ـ أ

ظهور التصور الميكانيكي

 الوثيقة ـ أ ـ توجد في وثيقة التلميذ بصيغة الـ PDF في نهاية المقال.

اقرأ النص )الوثيقة ـ أ ـ(، وبين ما هي الفكرة الحساسة، والدقيقة التي يشير إليها صاحب النص؟

ـ ما هي القضية في النص والتي أثير حولها الجدل الكبير؟

ـ متى فصل فيها ؟ ومن طرف من؟

الأجوبة:

الفكرة التي أثير حولها جدل كبير هي:

هل السرعة تبين إذا كانت هناك قوى خارجية مؤثرة على الجملة أم لا ؟

العالم غاليلي هو الذي فصل في القضية باعتماده الاستدلال العلمي بدلا من الاستدلال المبني على الحدس.

إذ أوضح أن السرعة لا تبيّن إن كانت هناك قوى خارجية أم لا تؤثر على الجملة، فإذا كان الجسم يتحرك بسرعة ثابتة فهو لا يخضع لأية قوة.

نص مبدأ العطالة (القانون الأول لنيوتن):

"يحافظ كل جسم على سكونه أو حركته المستقيمة المنتظمة إذا لم تتدخّل قوة لتغيير حالته الحركية".   

وعليه فإذا كانت حركة جسم ليست مستقيمة منتظمة فإنّه بالضرورة خاضع لقوة.

الوثيقة " ب"

مدخل إلى مفهوم القوة

السؤال الأول:

    لنتخيّل جسما (كرية مثلا)، ينتقل في الفضاء دون أن يخضع لتأثير أي قوة (لا الثقل ولا الاحتكاك ولا أية قوة أخرى)، ولنتخيّل أنّنا نأخذ له صورا متتالية خلال فترات زمنية متساوية (كل0.1 ثانية مثلا)، ثم نطابق كلّ هذه الصوّر.

حسب رأيك كيف تتوزّع المواضع المتتالية لمركز الجسم بالنسبة لبعضها البعض؟

يكون الجواب برسم على ورقة شفافة مرفوق بجملة توضيحية.

الاجابة:

السؤال الثاني:

    نواصل التخيّل، ونريد الآن أن تزداد سرعة مركز الجسم المذكور سابقا مع محافظته على مسار مستقيم.

أ ـ حسب رأيك، ما هو الشكل الجديد للتصوير المتعاقب لمركز الجسم؟ أرسم بعناية على ورق شفاف هذا الشكل.

ب ـ حسب رأيك، كيف يمكن التأثير على الجسم للحصول على هذه الحركة؟ مثّل بسهم على الرسم السابق، هذا التأثير، وأرفق رسمك بشرح مختصر.

الاجابة:

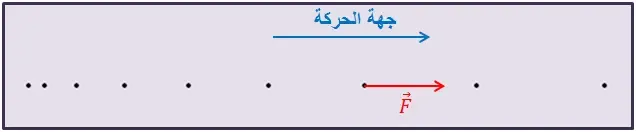
السؤال الثالث:

نريد هذه المرة أن تتناقص قيمة سرعة مركز الجسم المذكور سابقا مع محافظته على مسار مستقيم.

أ ـ نفس السؤال السابق.

ب ـ نفس السؤال السابق.  

الاجابة:

نتيجة:

- للحصول على سرعة متزايدة لجسم، يجب التأثير عليه بقوة تبقى منطبقة (أو مماسة) لمسار مركزه، ولها الجهة نفسها لحركته.

- للحصول على سرعة متناقصة لجسم يجب التأثير عليه بقوة تبقى منطبقة (أو مماسة) لمسار مركزه، ولها جهة معاكسة لحركته.

II ـ القوة الثابتة والحركات المستقيمة:

1 ـ حالة حركة مستقيمة منتظمة:

عند القيام بالتصوير المتعاقب لحركة عربة على نضد هوائي، ثم القيام بأخذ نقطة من العربة، ودراسة حركتها، تم الحصول على الوثيقة التالية:

حيث أن المدة الزمنية الفاصلة بين التقاطين متتاليين هي:

τ = 50 ms

1 ـ ماهي طبيعة مسار النقطة M ؟

2 ـ أوجد سرعة العربة عند المواضع M₁ ، M₂ ، M₃ ، M₄ ، M₅ ، M₆ ؟

3 ـ باختيار سلم رسم مناسب مثل أشعة السرعة في المواضع M₁ ، M₃ ، M₅ ؟

4 ـ أوجد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄  ؟ ماذا تلاحظ ؟

5 ـ مثل على ورقة ملمترية بيان تغيرات سرعة العربة بدلالة الزمن ؟

6 ـ استنتج سرعة العربة عند الموضعين M₀ ، M₇ ؟

7 ـ استنتج طبيعة حركة العربة ؟

8 ـ أكتب المعادلة الزمنية لحركة العربة ؟

أ ـ باعتبار مبدأ الازمنة منطبق على مبدأ الفواصل عند النقطة M₀ ؟

ب ـ باعتبار مبدأ الازمنة لحظة مرور العربة بالموضع M₂ ؟

الاجابة:

1 ـ المسار مستقيم

2 ـ ايجاد سرعة العربة عند المواضع M₁ ، M₂ ، M₃ ، M₄ ، M₅ ، M₆ :

لدينا:

$$v_1=v_{02}=\frac{M_0{M}_2}{2\tau }$$

ومنه:

$$v_1=\frac{24\times 10^{-2}}{100\times 10^{-3}}$$

ومنه:

$$v_1=2.4\text{m/s}$$

ومنه:

v₁ = 2,4 m.s^-1

و لدينا:

$$v_2=v_{13}=\frac{M_1{M}_3}{2\tau }$$

ومنه:

$$v_2=\frac{24\times 10^{-2}}{100\times 10^{-3}}$$

ومنه:

$$v_2=2.4\text{m/s}$$

ومنه:

v₂ = 2,4 m.s^-1

ولدينا:

$$v_3=v_{24}=\frac{M_2{M}_4}{2\tau }$$

ومنه:

$$v_3=\frac{24\times 10^{-2}}{100\times 10^{-3}}$$

ومنه:

$$v_3 = 2.4 \, \text{m/s}$$

ومنه:

v₃ = 2,4 m.s^-1

بنفس الطريقة نجد:

v₄ = 2,4 m.s^-1 ، v₅ = 2,4 m.s^-1 ، v₆ = 2,4 m.s^-1

3 ـ تمثيل أشعة السرعة في المواضع M₁ ، M₃ ، M₅ :

نأخذ مقياس الرسم  2,4 m.s^-1 → 1,5 cm

4 ـ ايجاد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄ :

لدينا: Δv₂ = v₃ – v₁

ومنه:

Δv₂ = 2,4 – 2,4 = 0

ولدينا: Δv₄ = v₅ – v₃

ومنه:

Δv₄ = 2,4 – 2,4 = 0

الملاحظة:

نلاحظ أن

Δv₂ = Δv₄ = 0

5 ـ تمثيل بيان تغيرات سرعة العربة بدلالة الزمن:

لدينا جدول القيم:

M7	M6	M5	M4	M3	M2	M1	M0	الموضع
350	300	250	200	150	100	50	0	t(ms)
	2,4	2,4	2,4	2,4	2,4	2,4		v(m.s-1)

6 ـ استنتاج سرعة العربة عند الموضعين M₀ ، M₇ :

عند تمديد الخط البياني نجد أن:

v₀ = 2,4 m.s^-1 ، v₇ = 2,4 m.s^-1

7 ـ استنتاج طبيعة حركة العربة:

حركة العربة مستقيمة منتظمة

8 ـ كتابة المعادلة الزمنية لحركة العربة

أ ـ باعتبار مبدأ الأزمنة منطبق على مبدأ الفواصل عند النقطة M₀ :

لدينا: x = v.t + x₀

اذا كان مبدأ الأزمنة منطبق على مبدأ الفواصل يعني أن 

x₀ = 0

ومنه نجد:

x = 2,4t (m)

ب ـ باعتبار مبدأ الأزمنة لحظة مرور العربة بالموضع M₂ :

في هذه الحالة نجد

x₀ = M₀M₂ = 24 cm = 0,24 m

ومنه:

x = 2,4t + 0,24 (m)

ب ـ حالة حركة مستقيمة متسارعة:

عند القيام بالتصوير المتعاقب لحركة عربة على نضد هوائي، ثم القيام بأخذ نقطة من العربة، ودراسة حركتها تم الحصول على الوثيقة التالية:

حيث أن المدة الزمنية الفاصلة بين التقاطين متتاليين هي:

τ = 50 ms

1 ـ ماهي طبيعة مسار النقطة M ؟

2 ـ أوجد سرعة العربة عند المواضع M₁ ، M₂ ، M₃ ، M₄ ، M₅ ، M₆ ؟

3 ـ باختيار سلم رسم مناسب مثل أشعة السرعة في المواضع M₁ ، M₃ ، M₅ ؟

4 ـ أوجد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄  ؟ ماذا تلاحظ ؟

5 ـ مثل على ورقة ملمترية بيان تغيرات سرعة العربة بدلالة الزمن ؟

6 ـ استنتج سرعة العربة عند الموضعين M₀ ، M₇ ؟

7 ـ استنتج طبيعة حركة العربة ؟

8 ـ هل العربة تخضع لقوة خلال حركتها ؟ اذا كان الجواب بنعم. أذكر خصائصها ومثلها في نقاط كيفية ؟

9 ـ اعط مثال من الواقع عن الحركة المستقيمة المتسارعة ؟

الاجابة:

1 ـ المسار مستقيم

2 ـ ايجاد سرعة العربة عند المواضع M₁ ، M₂ ، M₃ ، M₄ ، M₅ ، M₆ :

لدينا:

$$v_1 = v_2 = \frac{M_0 M_2}{2\tau}$$

ايجاد M₀M₂:

لدينا: 1,3 cm → 9 cm

ولدينا: M₀M₂ = 1,3 cm على الوثيقة ومنه M₀M₂ = 9 cm في الحقيقة

ومنه:

$$v_1 = \frac{9 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₁ = 0,9 m.s^-1

ولدينا:

$$v_2=v_{13}=\frac{M_1{M}_3}{2\tau }$$

ايجاد M₁M₃:

لدينا: 1,3 cm → 9 cm

ولدينا: M₁M₃ = 2,1 cm على الوثيقة ومنه M₁M₃ = 14,54 cm في الحقيقة.

ومنه:

$$v_2 = \frac{14.54 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₂ = 1,45 m.s^-1

ولدينا:

$$v_3 = v_4 = \frac{M_2 M_4}{2\tau}$$

ايجاد M₂M₄:

لدينا: 1,3 cm → 9 cm

ولدينا: M₂M₄ = 3 cm على الوثيقة ومنه M₂M₄ = 20,77 cm في الحقيقة.

ومنه:

$$v_3 = \frac{20.77 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₃ = 2,08 m.s^-1

ولدينا:

$$v_4 = v_5 = \frac{M_3 M_5}{2\tau}$$

ايجاد M₃M₅:

لدينا: 1,3 cm → 9 cm

ولدينا: M₃M₅ = 3,8 cm على الوثيقة ومنه M₃M₅ = 26,31 cm في الحقيقة.

ومنه:

$$v_4 = \frac{26.31 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₄ = 2,63 m.s^-1

ولدينا:

$$v_5 = v_6 = \frac{M_4 M_6}{2\tau}$$

ايجاد M₄M₆:

لدينا: 1,3 cm → 9 cm

ولدينا: M₄M₆ = 4,7 cm على الوثيقة ومنه M₄M₆ = 32,54 cm في الحقيقة.

ومنه:

$$v_5 = \frac{32.54 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₅ = 3,25 m.s^-1

ولدينا:

$$v_6 = v_7 = \frac{M_5 M_7}{2\tau}$$

ايجاد M₅M₇:

لدينا: 1,3 cm → 9 cm

ولدينا: M₅M₇ = 5,5 cm على الوثيقة ومنه M₅M₇ = 38,07 cm في الحقيقة.

ومنه:

$$v_6 = \frac{38.07 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₆ = 3,81 m.s^-1

3 ـ تمثيل أشعة السرعة في المواضع M₁ ، M₃ ، M₅ :

لدينا:

v₁ = 0,9 m.s^-1 ، v₃ = 2,08 m.s^-1 ، v₅ = 3,25 m.s^-1

نأخذ  0,9 m.s^-1 → 0,6 cm 

ومنه مقياس الرسم: 1 cm → 1,5 m.s^-1

ومنه:

v₁ → 0,6 cm ، v₃ → 1,4 cm ، v₅ → 2,2 cm

4 ـ ايجاد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄ :

لدينا: Δv₂ = v₃ – v₁

ومنه:

Δv₂ = 2,08 – 0,9 = 1,18 m.s^-1

ولدينا: Δv₄ = v₅ – v₃

ومنه:

Δv₄ = 3,25 – 2,08 = 1,17 m.s^-1

لدينا: 1 cm → 1,5 m.s^-1

ومنه: Δv₂ → 0,8 cm

ومنه: Δv₄ → 0,8 cm

يمكن ايجاد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄ بالاعتماد على الانشاء الهندسي للأشعة كما يلي:

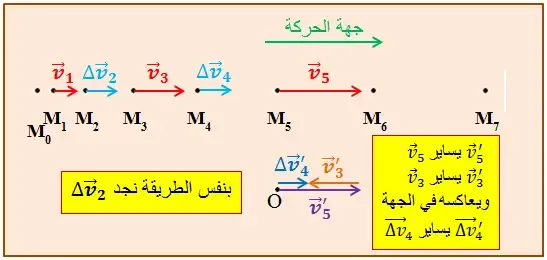
الملاحظة:

نلاحظ أن Δv₂ = Δv₄

5 ـ تمثيل بيان تغيرات سرعة العربة بدلالة الزمن:

لدينا جدول القيم:

M7	M6	M5	M4	M3	M2	M1	M0	الموضع
350	300	250	200	150	100	50	0	t(ms)
	3,81	3,25	2,63	2,08	1,45	0,9		v(m.s-1)

6 ـ استنتاج سرعة العربة عند الموضعين M₀ ، M₇ :

عند تمديد الخط البياني نجد أن:

v₀ = 0,3 m.s^-1 ، v₇ = 4,4 m.s^-1

7 ـ استنتاج طبيعة حركة العربة:

حركة العربة مستقيمة متسارعة بانتظام، لأن شعاع تغير السرعة في جهة الحركة، وقيمته ثابتة.  

8 ـ نعم العربة تخضع لقوة خلال حركتها، خصائصها من خصائص شعاع تغير السرعة، أي أن العربة تخضع خلال حركتها لقوة ثابتة في نفس جهة الحركة.

تمثيل شعاع القوة:

9 ـ مثال من الواقع عن الحركة المستقيمة المتسارعة:

حركة كرية تترك بدون سرعة ابتدائية من ارتفاع معين h عن سطح الأرض

3 ـ حالة حركة مستقيمة متباطئة:

عند القيام بالتصوير المتعاقب لحركة عربة على نضد هوائي ثم القيام بأخذ نقطة من العربة ودراسة حركتها تم الحصول على الوثيقة التالية:

حيث أن المدة الزمنية الفاصلة بين التقاطين متتاليين هي:

τ = 50 ms

1 ـ ماهي طبيعة مسار النقطة M ؟

2 ـ أوجد سرعة العربة عند المواضع M₁ ، M₂ ، M₃ ، M₄ ، M₅ ، M₆ ؟

3 ـ باختيار سلم رسم مناسب مثل أشعة السرعة في المواضع M₁ ، M₃ ، M₅ ؟

4 ـ أوجد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄ ؟ ماذا تلاحظ ؟

5 ـ مثل على ورقة ملمترية بيان تغيرات سرعة العربة بدلالة الزمن ؟

6 ـ استنتج سرعة العربة عند الموضعين M₀ ، M₇ ؟

7 ـ استنتج طبيعة حركة العربة ؟

8 ـ هل العربة تخضع لقوة خلال حركتها ؟ اذا كان الجواب بنعم . أذكر خصائصها ومثلها في نقاط كيفية ؟

الاجابة:

1 ـ المسار مستقيم.

2 ـ ايجاد سرعة العربة عند المواضع M₁ ، M₂ ، M₃ ، M₄ ، M₅ ، M₆ :

لدينا:

$$v_1 = v_2 = \frac{M_0 M_2}{2\tau}$$

ايجاد M₀M₂:

لدينا: 1,3 cm → 9 cm

ولدينا: M₀M₂ = 5,5 cm على الوثيقة ومنه M₀M₂ = 38,07 cm في الحقيقة.

ومنه:

$$v_1 = \frac{38.07 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₁ = 3,8 m.s^-1

ولدينا:

$$v_2 = v_3 = \frac{M_1 M_3}{2\tau}$$

ايجاد M₁M₃:

لدينا: 1,3 cm → 9 cm

ولدينا: M₁M₃ = 4,7 cm على الوثيقة ومنه M₁M₃ = 32,54 cm في الحقيقة.

ومنه:

$$v_2 = \frac{32.54 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₂ = 3,25 m.s^-1

ولدينا:

$$v_3 = v_4 = \frac{M_2 M_4}{2\tau}$$

ايجاد M₂M₄:

لدينا: 1,3 cm → 9 cm

ولدينا: M₂M₄ = 3,8 cm على الوثيقة ومنه M₂M₄ = 26,31 cm في الحقيقة.

ومنه:

$$v_3 = \frac{26.31 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₃ = 2,63 m.s^-1

ولدينا:

$$v_4 = v_5 = \frac{M_3 M_5}{2\tau}$$

ايجاد M₃M₅:

لدينا: 1,3 cm → 9 cm

ولدينا: M₃M₅ = 3 cm على الوثيقة ومنه M₃M₅ = 20,77 cm في الحقيقة.

ومنه:

$$v_4 = \frac{20.77 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₄ = 2,08 m.s^-1

ولدينا:

$$v_5 = v_6 = \frac{M_4 M_6}{2\tau}$$

ايجاد M₄M₆:

لدينا: 1,3 cm → 9 cm

ولدينا: M₄M₆ = 2,2 cm على الوثيقة ومنه M₄M₆ = 15,23 cm في الحقيقة.

ومنه:

$$v_5 = \frac{15.23 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₅ = 1,52 m.s^-1

ولدينا:

$$v_6 = v_7 = \frac{M_5 M_7}{2\tau}$$

ايجاد M₅M₇:

لدينا: 1,3 cm → 9 cm

ولدينا: M₅M₇ = 1,3 cm على الوثيقة ومنه M₅M₇ = 9 cm في الحقيقة.

ومنه:

$$v_6 = \frac{9 \times 10^{-2}}{100 \times 10^{-3}}$$

ومنه:

v₆ = 0,9 m.s^-1

3 ـ تمثيل أشعة السرعة في المواضع M₁ ، M₃ ، M₅ :

لدينا:

v₁ = 3,8 m.s^-1 ، v₃ = 2,63 m.s^-1 ، v₅ = 1,52 m.s^-1

نأخذ مقياس الرسم: 1 cm → 1,7 m.s^-1

ومنه:

v₁ → 2,2 cm ، v₃ → 1,5 cm ، v₅ → 0,9 cm

4 ـ ايجاد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄ :

لدينا: Δv₂ = v₃ – v₁

ومنه:

Δv₂ = 2,63 – 3,8 = - 1,17 m.s^-1

ولدينا: Δv₄ = v₅ – v₃

ومنه:

Δv₄ = 1,52 – 2,63 = - 1,11 m.s^-1

لدينا: 1 cm → 1,7 m.s^-1

ومنه:

Δv₂ → 0,7 cm 

يمثل الشعاع عكس جهة الحركة لأن

Δv₂ < 0 

ومنه:

Δv₄ → 0,7 cm 

يمثل الشعاع عكس جهة الحركة لأن

Δv₄ < 0

يمكن ايجاد قيمتي شعاعي تغير السرعة عند الموضعين M₂ ، M₄ بالاعتماد على الانشاء الهندسي للأشعة كما يلي:

الملاحظة:

نلاحظ أن Δv₂ = Δv₄

5 ـ تمثيل بيان تغيرات سرعة العربة بدلالة الزمن:

لدينا جدول القيم:

M7	M6	M5	M4	M3	M2	M1	M0	الموضع
350	300	250	200	150	100	50	0	t(ms)
	0,9	1,52	2,08	2,63	3,25	3,8		v(m.s-1)

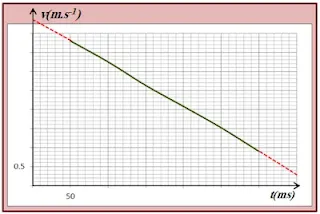
6 ـ استنتاج سرعة العربة عند الموضعين M₀ ، M₇ :

عند تمديد الخط البياني نجد أن:

v₀ = 4,4 m.s^-1 ، v₇ = 0,3 m.s^-1

7 ـ استنتاج طبيعة حركة العربة:

حركة العربة مستقيمة متباطئة بانتظام لأن شعاع تغير السرعة عكس جهة الحركة وقيمته ثابتة.  

8 ـ نعم العربة تخضع لقوة خلال حركتها، خصائصها من خصائص شعاع تغير السرعة، أي أن العربة تخضع خلال حركتها لقوة ثابتة جهتها عكس جهة الحركة.

تمثيل شعاع القوة:

وثيقة التلميذ بصيغة الـ PDF

1/ البطاقـة التربويـة لدرس القوة والحركات المستقيمة بصيغة الـ PDF (نموذج عادي)

2/ البطاقـة التربويـة لدرس القوة والحركات المستقيمة بصيغة الـ PDF (نموذج مخصص)