حلول تمارين الكتاب المدرسي حول التحولات النووية

حل التمرين 3 صفحة 102 من وحدة التحولات النووية:

1 ـ إعطاء رموز أنوية خمسة نظائر للبوتاسيوم:

$${}_{19}^{42}K,{}_{19}^{41}K,{}_{19}^{40}K,{}_{19}^{39}K,{}_{19}^{38}K$$

حيث أن البوتاسيوم له 23 نظير منها ثلاث نظائر طبيعية هي:

$${}_{19}^{41}\text{K};{}_{19}^{40}\text{K};{}_{19}^{39}\text{K}$$

2 ـ النواة

$${}_{20}^{40}\text{X}$$

لا تمثل نظيرا للبوتاسيوم لأنه ليس لها نفس العدد الذري للبوتاسيوم.

3 ـ حساب الوفرة النظائرية للبوتاسيوم:

نفرض أن نسبة تواجد النظير 39 هي x ، ونسبة تواجد النظير41 هي (100 – x)

ومنه نجد:

$$M_K=\frac{38,96\cdot x}{100}+\frac{40,96\cdot (100-x)}{100}=39,10$$

ومنه: 0,3896x + 40,96 - 0,4096x = 39,10

ومنه: 0,02x = 1,86 ومنه: x = 93%

أي أن نسبة تواجد النظير 39 هي 93% ، ونسبة تواجد النظير 41 هي 7%

حل التمرين 4 صفحة 102 من وحدة التحولات النووية:

1 ـ العنصر X نظير للبيريليوم لأن لهما نفس العدد الذري Z

2 ـ النواة X غير مستقرة لأنها لا تنتمي الى وادي الاستقرار.

3 ـ نمط التفكك الذي يمكن أن يحدث للنواة X هوβˉ

4 ـ معادلة التفكك النووي:

$${}_4^{10}\text{Be}\to {}_5^{10}\text{B}+{}_{-1}^0{\text{e}}^{-}+\bar{\nu }$$

ومنه النواة التي تشكلها بعد تفككها هي نواة البور.

حل التمرين 5 صفحة 102 من وحدة التحولات النووية:

${}^{226}_{88}\text{Ra} \rightarrow {}^{222}_{86}\text{Rn} + {}^{4}_{2}\text{He}$

${}^{12}_{7}\text{N} \rightarrow {}^{12}_{6}\text{C} + {}^{0}_{1}\text{e}$

${}^{14}_{6}\text{C} \rightarrow {}^{14}_{7}\text{N} + {}^{0}_{-1}\text{e}$

${}^{174}_{73}\text{Ta} \rightarrow {}^{174}_{72}\text{Hf} + {}^{0}_{1}\text{e}$

${}^{213}_{84}\text{Po} \rightarrow {}^{209}_{82}\text{Pb} + {}^{4}_{2}\text{He}$

${}_{72}^{174}\text{Hf}\to {}_{70}^{170}\text{Yb}+{}_2^4\text{He}$

حل التمرين 6 صفحة 102 من وحدة التحولات النووية:

1 ـ تحديد الأنماط الاشعاعية:

النمط (1) هو α لأن عدد البروتونات نقص بـ 2 وعدد النيترونات نقص بـ 2.

النمط (2) هوβ⁺ لأن عدد البروتونات نقص بـ 1 وعدد النيترونات إزداد بـ 1.

النمط (3) هوβˉ لأن عدد البروتونات إزداد بـ 1 وعدد النيترونات نقص بـ 1.

2 ـ تتميز الأنوية المستقرة من أجل Z ˂ 20 بتساوي عددي البروتونات والنيترونات.

3 ـ من مخطط سيقري N = f(Z)

نلاحظ أن النظير

$${}_{70}^{152}\text{Yb}$$

يقع تحت وادي الاستقرار، ومنه فهو يتفكك وفق النمط  α أو⁺β لكي يعطي نواة إبن قريبة نسبيا من وادي الاستقرار.

$${}_{70}^{152}\text{Yb}\to {}_{69}^{152}\text{Tm}+{}_{+1}^0{\text{e}}^{+}+\nu$$

4 ـ النواة الابن مشعة لأنها لا تنتمي الى وادي الاستقرار.

5 ـ النواتان

$${}_{54}^{139}\text{Xe};{}_{38}^{98}\text{Sr}$$

تقعان فوق وادي الاستقرار في المخطط N = f(Z)، لهذا تتفككان حسب النمط βˉ

حل التمرين 8 صفحة 103 من وحدة التحولات النووية:

1 ـ يعطى قانون التناقص الاشعاعي بالعلاقة: N(t) = N₀e^-λt

حيث N₀ عدد الأنوية الابتدائية.

2 ـ التعبير عن ثابت الزمن بدلالة زمن نصف العمر:

لدينا:

$$N(t_{1/2}) = N_0 e^{-\frac{t_{1/2}}{\tau}} = \frac{N_0}{2}$$

ومنه:

$$N(t) = N_0 e^{-\frac{t}{\tau}}$$

ولأن:

$$\frac{N_0}{2} = N_0 e^{-\frac{t_{1/2}}{\tau}}$$

ومنه:

$$\ln e^{-\frac{t_{1/2}}{\tau}} = \ln \frac{1}{2}$$

ومنه:

$$e^{-\frac{t_{1/2}}{\tau}} = \frac{1}{2}$$

ومنه:

$$-\frac{t_{1/2}}{\tau} = \ln \frac{1}{2}$$

ومنه:

$$\tau =\frac{t_{1\mathrm{/}2}}{\ln 2}\text{ومنها}{t}_{1\mathrm{/}2}=\tau \ln 2$$

3 ـ حساب كتلة الفرنسيوم المتبقية بعد1 ساعة:

لدينا: m = m₀e^-λt

نحسب λ:

لدينا:

$$\lambda = \frac{1}{\tau} = \frac{\ln 2}{t_{1/2}}$$

ومنه:

$$\lambda =\frac{0.69}{22}=3.13\times {10}^{-2}{\text{min}}^{-1}$$

ومنه: m = 1,0×10^-13e^-0,0313×60 ومنه: m = 1,52×10^-14 g

4 ـ حساب عدد الأنوية المتبقية:

لدينا:

$$N = \frac{m \cdot N_A}{M}$$

ومنه:

$$N = \frac{1.52 \times 10^{-14} \cdot 6.023 \times 10^{23}}{235}$$

ومنه:

$$N=4.1\times {10}^7\text{ noyaux}$$

حساب نشاط الكتلة المتبقية:

لدينا:

$$A = \lambda \cdot N$$

ومنه:

$$A = \lambda \cdot N = \frac{0.69}{22 \times 60} \cdot 4.1 \times 10^7$$

ومنه:

$$A=2.14\times {10}^4\text{ Bq}$$

حل التمرين 9 صفحة 103 من وحدة التحولات النووية:

1 ـ إتمام معادلة التفكك النووي:

$${}_{15}^{32}\text{P}\to {}_{16}^{32}\text{S}+{}_{-1}^0{\text{e}}^{-}+\bar{\nu }$$

2 ـ حساب العدد الابتدائي لأنوية الفوسفور 32:

لدينا:

$$m = m_0 \cdot \frac{53}{100} = 1 \cdot \frac{53}{100} = 0.53 \ \text{g}$$

ولدينا:

$$n = \frac{m}{M} = \frac{0.53}{32} = 1.65 \times 10^{-2} \ \text{mol}$$

ولدينا:

$$N_0 = n \cdot N_A = 1.65 \times 10^{-2} \cdot 6.023 \times 10^{23}$$ومنه:
$$N_0=9.9\times {10}^{21}\text{ noyaux}$$

3 ـ بالاعتماد على العلاقة:

$$N(t)=N_0\cdot e^{-\frac{t\cdot \ln 2}{t_{1\mathrm{/}2}}}$$

نحسب عدد الأنوية في كل لحظة.

40	35	30	25	20	15	10	5	0	t(j)
1,4	1,8	2,3	2,9	3,8	4,8	6,1	7,8	9,9	N×1021

 4 ـ تمثيل بيان الدالة: N = f(t)

5 ـ بالاعتماد على البيان نجد: τ ≈ 21 jours

حل التمرين 10 صفحة 103 من وحدة التحولات النووية:

1 ـ كتابة معادلة التفكك:

$${}_{83}^{212}\text{Bi}\to {}_{81}^{208}\text{Tl}+{}_2^4\text{He}$$

2 ـ حساب ثابت النشاط الاشعاعي λ:

لدينا:

$$\lambda = \frac{\ln 2}{t_{1/2}}$$ $$\lambda = \frac{0.693}{60 \times 60} = 1.92 \times 10^{-4} \ \text{s}^{-1}$$

3 ـ حساب النشاط الاشعاعي:

$$A = \frac{\Delta N}{\Delta t} = \frac{1.88 \times 10^{17}}{6} = 3.1 \times 10^{16} \ \text{Bq}$$

4 ـ ايجاد العدد المتوسط للأنوية المشعة في لحظة القياس:

لدينا:

$$A = \lambda \cdot N \quad \Rightarrow \quad N = \frac{A}{\lambda}$$ $$N=\frac{3.1\times {10}^{16}}{1.92\times {10}^{-4}}=1.61\times {10}^{20}\text{ noyaux}$$

5 ـ ايجاد كتلة البيزموث الحاضرة في المنبع في هذه اللحظة:

لدينا:

$$m = n \cdot M \quad \text{و} \quad n = \frac{N}{N_A} \quad \Rightarrow \quad m = \frac{N \cdot M}{N_A}$$

التطبيق العددي:

$$m=\frac{1.61\times {10}^{20}\cdot 212}{6.02\times {10}^{23}}=5.67\times {10}^{-2}\text{ g}$$

6 ـ حساب حجم الهيليوم الناتج:

نعتبر أن النشاط يبقى ثابتا خلال دقيقة ومنه:

ΔA = 3,1×10¹⁶×60 = 1,86×10¹⁸Bq

لدينا في كل تفكك تنتج نواة هيليوم، ومنه عدد أنوية الهيليوم الناتجة هو:

N = 1,86×10¹⁸ noyaux

نحسب كمية مادة الهيليوم الناتجة:

$$n = \frac{N}{N_A} = \frac{1.86 \times 10^{18}}{6.02 \times 10^{23}} = 3.1 \times 10^{-6} \ \text{mol}$$

ومنه حجم الهيليوم الناتج في الشروط العادية هو:

V_He = n.V_M = 3,1×10^-6×22,4 = 6,94×10^-5 L

7 ـ حساب نشاط العينة خلال لحظات زمنية مختلفة:

لدينا: A(t) = A₀.e^-λt 

ولدينا: λ = 1,92×10^-4s^-1 ، A₀ = 3,1×10¹⁶Bq 

ومنه نجد:

60×3600	24×3600	3600	t(s)
4,7×10-2	2,3×109	1,55×1016	A(Bq)

 نحسب عدد الأنوية المتبقية عند 60 ساعة:

$$N^{\mathrm{\prime }}=\frac{A}{\lambda }=\frac{4.7\times {10}^{-2}}{1.9\times {10}^{-4}}=245\text{ noyaux}$$

نحسب النسبة N'/N:

$$\frac{N'}{N} = \frac{245}{1.61 \times 10^{16}} = 1.5 \times 10^{-14} \approx 0$$

ومنه نعتبر أن العينة اختفت ولم تصبح تشع.

حل التمرين 11 صفحة 104 من وحدة التحولات النووية:

1 ـ حساب المدة اللازمة لتفكك 9/10 من الكتلة m₀:

لدينا: m = m₀e^-λt

عند تفكك 9/10 من m₀ تصبح الكتلة المتبقية هي 1/10 من m₀ ومنه نجد:

$$\frac{m_0}{10} = m_0 \cdot e^{-\lambda t}$$

بقسمة الطرفين على $m_0$، نحصل على:

$$\frac{1}{10} = e^{-\lambda t}$$

وبأخذ اللوغاريتم الطبيعي للطرفين، ينتج:

$$\ln\left(\frac{1}{10}\right) = \ln\left(e^{-\lambda t}\right)$$

وبما أن $\ln(e^x) = x$، فإن:

$$-\lambda t = \ln\left(\frac{1}{10}\right)$$

وبالتالي:

$$\lambda t = 2.3$$

ومنه:

$$t=\frac{2.3}{\lambda }$$

نحسب λ:

لدينا:

$$\lambda =\frac{\ln (2)}{t_{1\mathrm{/}2}}$$

ومنه:

$$\lambda = \frac{0.693}{3.825 \times 24 \times 3600}$$

ومنه:

$$\lambda =2.1\times {10}^{-6}{\text{s}}^{-1}$$

من خلال المعادلة:

$$t = \frac{2.3}{2.1 \times 10^{-6}} = 1,095,238.1 \, \text{s}$$

وبعد تحويل الزمن إلى الأيام:

$$t=\frac{1,095,238.1}{86400}\approx 12.67\text{jours}$$

2 ـ حساب كمية مادة أنوية الرادون:

لدينا:

$$PV = nRT$$

ومنه:

$$n = \frac{PV}{RT}$$

ومنه:

$$n = \frac{1{,}0 \times 10^4 \times 2 \times 10^{-6}}{8{,}32 \times 303}$$

ومنه:

$$n=\mathrm{7,93}\times {10}^{-6}\text{mol}$$

3 ـ إيجاد عدد الأنوية المشعة N₀:

لدينا: N₀ = n.N_A ومنه: N₀ = 7,93×10^-6×6,02×10²³ 

ومنه: N₀ = 4,77×10¹⁸ noyaux

4 ـ تحديد النشاط الابتدائي:

A₀ = λ.N₀ ومنه: A₀ = 2,1×10^-6×4,77×10¹⁸ 

ومنه: A₀ = 10¹³ Bq

تحديد النشاط بعد 100 يوم:

A = A₀e^-λt ومنه: A = 1,3×10⁵ Bq

حل التمرين 12 صفحة 104 من وحدة التحولات النووية:

لدينا:

$$A(t) = A_0 e^{-\lambda t}$$

ولدينا:

$$\lambda = \frac{1}{\tau} = \frac{\ln 2}{t_{1/2}}$$

ومنه:

$$A(t)=A_0\cdot e^{-t\cdot \ln 2\mathrm{/}{t}_{1\mathrm{/}2}}$$

كما أننا نلاحظ أن اللحظات الزمنية المعطاة تمثل مضاعفات t_1/2 ومنه نجد:

40	32	24	16	8	0	t(j)
1	2	4	8	16	32	A(Bq)×106

 التمثيل البياني لـ A(t) = A₀e^-λt:

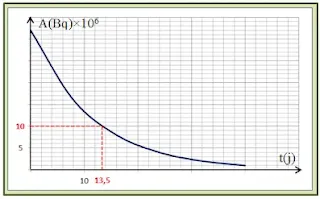
2 ـ تحديد اللحظة التي يصبح عندها النشاط مساويا لـ 10×10⁶ Bq:

بالاعتماد على البيان السابق نجد: t ≈ 13,5 j

3 ـ رسم المنحنى lnA = f(t):

لدينا:

40	32	24	16	8	0	t(j)
13,81	14,51	15,20	15,89	16,59	17,28	lnA

4 ـ استنتاج قيمة λ لليود 131:

لدينا: A(t) = A₀e^-λt  ومنه: lnA(t) = lnA₀e^-λt 

ومنه: lnA(t) = lnA₀ – λt  ومنه: lnA(t) = – λt + lnA₀ → (1)

ومن البيان نجد: lnA(t) = a.t + lnA₀ → (2) حيث a يمثل ميل الخط البياني

من (1) و (2) نجد: λ = - a

ومنه:

$$\lambda = \frac{17{,}28 - 13{,}81}{40 \times 24 \times 3600} = 1{,}003 \times 10^{-6} \, \text{s}^{-1}$$

حل التمرين 17 صفحة 106 من وحدة التحولات النووية:

1 ـ معادلة التفكك:

$${}_6^{14}\text{C}\to {}_7^{14}\text{N}+{}_{-1}^0{e}^{-}+\bar{\nu }$$

قانونا الانحفاظ المستعملين هما قانونا صودي، (إنحفاظ العدد الذري و إنحفاظ العدد الكتلي).

أما نمط التفكك فهوβˉ

الزمن اللازم لتناقص كمية الكربون 14 الى النصف هو t_1/2 = 5570 ans

3 ـ العلاقة هي:

$$t=\frac{1}{\lambda }\ln \left(\frac{A_0}{A(t)}\right)$$

4 ـ تعيين تاريخ تصنيع التابوت:

لدينا:

$$\frac{1}{\lambda} = \tau = \frac{t_{1/2}}{\ln 2}$$

ومنه:

$$t = \frac{t_{1/2}}{\ln 2} \cdot \ln\left(\frac{A_0}{A(t)}\right)$$

ومنه:

$$t = \frac{5570}{0{,}69} \cdot \ln\left(\frac{102}{70}\right)$$

ومنه:

$$t = 3039 \, \text{ans}$$