إنكسار الضوء. الاجابة عن أهم الاسئلة

يُعرف انكسار الضوء، بأنه الظاهرة الفيزيائية التي تحدث عندما ينتقل شعاع الضوء من وسط شفاف إلى وسط آخر، مختلف في الكثافة البصرية، مما يؤدي إلى تغيّر سرعة الضوء، وانحراف مساره عند السطح الفاصل بين الوسطين. مثال شائع على هذه الظاهرة هو انحناء الضوء، عند انتقاله من الهواء إلى الماء.

ينشأ انكسار الضوء بسبب اختلاف معامل الانكسار بين الوسيطين. معامل الانكسار هو مقياس يحدد مدى بطء الضوء، عند مروره عبر مادة معينة مقارنة بسرعته في الفراغ. كلما زاد الفرق في معامل الانكسار بين الوسيطين، كان الانحراف أكثر وضوحًا.

ملاحظة: توجد وثيقة التلميذ بصيغة الـ PDF في نهاية المقال

I ـ تذكير:

أ ـ الانتشار المستقيم للضوء:  

تجربة:

نحقق التركيب التجريبي التالي:

ـ عند تحريك إحدى الصفائح هل تصل الاشعة الى العين؟

عند تحريك إحدى الصفائح نلاحظ أن الأشعة لا تصل الى العين.

نتيجة:

ينتشر الضوء في جميع الاتجاهات وفق خطوط مستقيمة.

ب ـ الحزمة الضوئية: 

هي مجموعة من الاشعة الضوئية الصادرة من منبع ضوئي واحد.

جـ ـ الاوساط الضوئية:

ـ الى كم صنف تصنف الأوساط الضوئية ؟

تصنف الأوساط الضوئية الى ثلاثة أصناف.

ـ أذكر الأوساط الضوئية ؟

الأوساط الشفافة، الأوساط الشافة، الأوساط العاتمة.

ـ عرف الأوساط الضوئية مع اعطاء أمثلة مناسبة ؟

الأوساط الشفافة: 

وهي أوساط تسمح بمرور الضوء، ونرى الاشياء من خلالها بوضوح، مثل الزجاج الاملس و الهواء و الماء ...

الأوساط الشافة: 

وهي أوساط تسمح بمرور الضوء، وتكون رؤية الاشياء من خلالها غير واضحة، مثل الزجاج الخشن والورق المبلل بالزيت والضباب ...

الأوساط العاتمة: 

وهي أوساط تمنع مرور الضوء، ولا نرى الاشياء من خلالها، مثل الخشب والحديد ...

د ـ تذكير بظاهرة انعكاس الضوء:

* تعريف المرآة المستوية:

هي عبارة عن سطح مصقول، (مستوي تماما). تعكس معظم الأشعة الساقطة عليها بشكل منتظم، المرآة المستوية عبارة عن لوح زجاجي مستوي، أحد سطحيه مغطى بمادة عاكسة للضوء، وهي أكثر أنواع المرايا شيوعًا، وتُستخدم بكثرة في الحياة اليومية في مختلف الأماكن من المنازل، والمتاجر وغيرها.

ـ ضع رسما تخطيطيا توضح من خلاله ظاهرة الانعكاس؟

ـ أذكر قانونا الانعكاس؟

1/ الشعاع الوارد، والشعاع المنعكس، والناظم للسطح في نقطة الورود، تقع في نفس المستوي.

2/ زاوية الانعكاس تقايس زاوية الورود. إذا كانت زاوية الورود معدومة فإن زاوية الانعكاس معدومة.

فيديو يوضح تجربة انعكاس الضوء

II ـ ظاهرة الانكسار:

1 ـ قانونا الانكسار، قرينة الانكسار:

الانكسار الضوئي: 

هو انحراف الضوء عن مساره، عند انتقاله من وسط شفاف إلى وسط شفاف آخر.

قانونا الانكسار:

القانون الأول:

يقع كل من الشعاع الوارد، والشعاع المنكسر، والناظم للسطح الكاسر، عند نقطة الورود في نفس المستوي.

القانون الثاني: 

من أجل وسطين شفافين نسبة "sin" زاوية الورود، الى "sin" زاوية الانكسار ثابتة أي:

  sin i/sin r = cte

ـ ماذا يسمى الثابت؟

يسمى الثابت "القرينة النسبية لانكسار الضوء، للوسط الثاني بالنسبة للوسط الأول"

ـ كيف يرمز لهاذا الثابت؟

يرمز له بالرمزn_2/1  

ـ ماذا يساوي بدلالة قرينة انكسار الوسط الأول، وقرينة انكسار الوسط الثاني؟

يساوي نسبة قرينة انكسار الوسط الثاني إلى قرينة انكسار الوسط الأول ونكتب:

n_2/1= n₂/n₁ 

ـ كيف تصبح عبارة القانون الثاني للانكسار؟

تصبح عبارة القانون الثاني للانكسار من الشكل:

 n₁ sin i = n₂ sin r

- إذا كان الوسط الأول هو الهواء تدعى هذه النسبة، قرينة الانكسار المطلقة للوسط الثاني ويكتب القانون الثاني للانكسار: sin i = n sin r 

فيديو يوضح تجربة انكسار الضوء

ـ وضح كيفية انتقال الشعاع الضوئي من وسط أقل كسرا الى وسط أشد كسرا ؟

عندما ينتقل الضوء من وسط أقل كسرا إلى وسط أشد كسرا، يقترب الشعاع المنكسر من الناظم، وينحرف عن مساره بزاوية تدعى زاوية الانحراف يرمز لها بـ D

ـ وضح كيفية انتقال الشعاع الضوئي من وسط أشد كسرا الى وسط أقل كسرا ؟

عندما ينتقل الضوء من وسط أشد كسرا إلى وسط أقل كسرا، يبتعد الشعاع المنكسر عن الناظم.

2 ـ ظاهرتي الانكسار الحدي و الانعكاس الكلي:

أ ـ ظاهرة الانكسار الحدي:

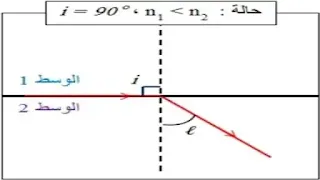
- في الحالة التي ينتقل فيها الضوء من وسط أقل كسرا إلى وسط أشد كسرا، فإن زاوية الانكسار تأخذ قيمة حدية "ℓ" عندما تصل زاوية الورود إلى القيمة °90.

- في الحالة التي ينتقل فيها الضوء من الهواء إلى وسط شفاف قرينة انكساره n، تحسب الزاوية الحدية بالعلاقة: 

sin ℓ  = 1/n

ب ـ ظاهرة الانعكاس الكلي:

- في الحالة التي يرد فيها الضوء من وسط أشد كسرا الى وسط أقل كسرا، نميز ثلاث حالات:

1/ اذا كان i<ℓ يبرز الشعاع المنكسر مبتعدا عن الناظم.

2/ اذا كان i=ℓ يبرز الشعاع المنكسر منطبقا على السطح الكاسر.

3/ اذا كان i>ℓ يحدث انعكاس كلي.

ينعكس كليا اذا كان: i > ℓ

III ـ انحراف الضوء بالموشور:

1 ـ تعاريف:

ـ الموشور وسط ضوئي شفاف، ومتجانس محدد بسطحين مستويين غير متوازيين.

ـ نسمي السطحين وجهي الموشور، و خط تقاطعهما يدعى حرف الموشور.

ـ الزاوية المحصورة بين السطحين تسمى زاوية الموشور، ورمزها A.

ـ يمثل الموشور على شكل مثلث.

2 ـ تجارب اولية (الانحراف و التبدد):

نشاط 1:

نسقط أشعة الشمس على أحد وجهي موشور.

ـ ماذا نلاحظ ؟

نلاحظ بروزها من الوجه الثاني على شكل حزمة ملونة بألوان الطيف.

نشاط 2:

 نعيد نفس التجربة السابقة، وذلك بوضع مرشح ملون (أحمر مثلا) مزود بحاجز عاتم به شق. 

ـ ماذا نلاحظ ؟

نلاحظ بروز حزمة ضوئية حمراء اللـون.

نتيجة:

يحلل الموشور الضوء الأبيض إلى ألوانه الأصلية (ألوان الطيف المرئية)، تدعى هذه الظاهرة بتبدد الضوء.

فيديو يوضح تجربة انحراف الضوء بالموشور

3 ـ الدراسة الكمية لانحراف الضوء في الموشور:

لدراسة مسير الشعاع الضوئي عبر الموشور، نستعمل منبع ضوئي وحيد اللون (لتفادي حدوث ظاهرة التبدد)، وموشور قرينة انكساره n معروفة نضع الموشور فوق ورقة بيضاء، ثم نسقط شعاعا ضوئيا على أحد وجهيه، بحيث يبرز من الوجه الآخر كما في الشكل التالي:

ـ ماذا نسمي i₁ ،  i₂و D ؟

نسمي i₁ زاوية الورود و  i₂زاوية البروز و D زاوية الانحراف.

هندسيا نجد أن : = i₁ + i₂ - A   D

                            = r₁ + r₂ A

ـ اثبت العلاقة: A = r₁ + r₂ ؟

اثبات العلاقة : A = r₁ + r₂

لدينا: A + α + β = 180 →(1)

و لدينا: r₁ + α + 90 = 180 →(2)

و لدينا: r₂ + β + 90 = 180 →(3)

من (2) نجد: α = 90 – r₁

و من (3) نجد: β = 90 – r₂

بالتعويض في (1) نجد: A + 90 – r₁ + 90 – r₂ = 180

و منه: A – r₁ – r₂ + 180 = 180

ومنه: A – r₁ – r₂ = 0 و منه: A = r₁ + r₂

ـ اثبت العلاقة: D = i₁ + i₂ – A ؟

اثبات العلاقة: D = i₁ + i₂ – A

لدينا: i₁ = r₁ + D₁ →(1)

و لدينا: i₂ = r₂ + D₂ →(2)

بجمع (1) و (2) نجد: i₁ + i₂ = r₁ + r₂ + D₁ + D₂

لدينا: D₁ + D₂ = D و A = r₁ + r₂

و منه: i₁ + i₂ = A + D  و منه: D = i₁ + i₂ – A

نتيجة: 

مما سبق يمكن استنتاج علاقات الموشور التالية:

sin i₁ = n sin r₁  ، n sin r₂ = sin i₂  ،= i₁ + i₂ - A   D ، A= r₁ + r₂

4 ـ شرطا بروز شعاع ضوئي من الموشور:

الشرط الأول:

لا يمكن لأي شعاع وارد أن يخرج من موشور، إلا إذا كانت زاوية هذا الموشور A أقل من ضعفي الزاوية الحدية للانكسار، ونكتب: A ≤ 2l.

ـ اثبت العلاقة: A ≤ 2l ؟

اثبات العلاقة:  A ≤ 2l

حتى يبرز الشعاع الوارد من الموشور، ينبغي أن يكون r₁ ≤ l ، r₂ ≤ l 

ومنه: r₁ + r₂ ≤ 2l

ولدينا: A= r₁ + r₂ ومنه: A ≤ 2l

الشرط الثاني:

القيم اللازم إعطائها لزاوية الورود حتى يكون هناك بروز، بعد تحقق الشرط الأول، هي القيم التي تحقق العلاقة التالية: 

sin i₀ ≥ n sin (A - l)

حيث: i₀ هي أدنى قيمة لزاوية الورود على الوجه الأول الموشور.

ـ اثبت العلاقة: sin i₀ ≥ n sin(A - l) ؟

اثبات العلاقة: sin i₀ ≥ n sin(A - l)

مما سبق حتي يحدث بروز للشعاع الضوئي من الموشور، يجب أن يكون r₂ ≤ l 

ولدينا: A= r₁ + r₂

ومنه: r₂ = A – r₁ ومنه: A – r₁ ≤ l ومنه: r₁ – A ≥ - l ومنه: r₁ ≥ A – l  

ومنه: sin r₁ ≥ sin(A – l) ، 

بضرب الطرفين في n نجد: n sin r₁ ≥ n sin(A – l)

ولدينا: n sin r₁ = sin i₁ ومنه: sin i₁ ≥ n sin(A – l)

من أجل i₁ = i₀ نجد: sin i₀ ≥ n sin(A – l)

5 ـ زاوية الانحراف الأدنى:

نحصل على أدنى انحراف  D_mللشعاع البارز، عندما تكون الزاويتان  i₁و i₂متساويتان:

$$\sin \left(\frac{D_m+A}{2}\right)=n\sin \left(\frac{A}{2}\right)$$

حيث:

$$i_1=i_2=\frac{D_m+A}{2}$$

اثبات العلاقة:

$$\sin \left(\frac{D_m+A}{2}\right)=n\sin \left(\frac{A}{2}\right)$$

لدينا: sin i₁ = n sin r₁ → (1)

ولدينا: D = i₁ + i₂ – A ، 

من أجل i₁ = i₂ نتحصل على أدنى انحراف D_m ، 

ونجد: D_m = 2i₁ – A

ومنه: 2i₁ = D_m + A  ومنه:

$$i_1=\frac{D_m+A}{2}\text{...... (2)}$$

ولدينا: i₁ = r₁ + D₁ ومنه: r₁ = i₁ – D₁ حيث:

$$i_1 = \frac{D_m + A}{2}$$ $$D_1=\frac{D_m}{2}$$

ومنه:

$$r_1 = \frac{D_m + A}{2} - \frac{D_m}{2}$$ $$r_1 = \frac{D_m + A - D_m}{2}$$

$$r_1=\frac{A}{2}\text{...... (3)}$$

بتعويض (2) و (3) في (1) نجد:

$$\sin \left(\frac{D_m+A}{2}\right)=n\sin \left(\frac{A}{2}\right)$$

ـ اذا كان

 ماذا يحدث للشعاع الضوئي    0 ≤ i₁ ≤ i₀

يحدث انعكاس كلي للشعاع الضوئي الساقط على الوجه الثاني للموشور

وثيقة التلميذ بصيغة الـ PDF