حلول تمارين الكتاب المدرسي حول الطاقة الكامنة

حلول تمارين الكتاب المدرسي حول الطاقة الكامنة، دليلاً عمليًا للطلاب لفهم الطاقة الكامنة بعمق، وتطبيق القوانين الفيزيائية المتعلقة بها، مثل قانون حفظ الطاقة، وعلاقة الطاقة الكامنة بالطاقة الحركية.

حل التمرين الأول حول الطاقة الكامنة صفحة 86

اختيار الجواب الصحيح:

ـ تكتب عبارة الطاقة الكامنة الثقالية على الشكل (أ) E_PP = Mgz ، اذا كان المحور (OZ) موجه نحو الاعلى.

ـ شرط كتابة هذه العبارة هو اختيار وضع مرجعي، تكون عنده الطاقة الكامنة الثقالية معدومة (يوافق E_pp = 0).

ـ الطاقة الكامنة الثقالية تتعلق بمرجع الدراسة أي باختيار مبدأ المحور.

ـ التغير في الطاقة الكامنة الثقالية لا يتعلق بمرجع الدراسة.

ـ عبارة التغير في الطاقة الكامنة الثقالية هي:

$$\mathrm{\Delta }{E}_{pp}=-W_{AB}(\vec{P})$$

ـ عندما نقذف جسما نحو الأعلى، فإن طاقته الكامنة الثقالية تزداد (لأن الارتفاع يزداد).  

ـ عندما ينتقل جسم على مستو أفقي، فإن طاقته الكامنة الثقالية تبقى ثابتة (لأن الارتفاع يبقى ثابتا).

حل التمرين الثاني حول الطاقة الكامنة صفحة 86

نعني بالعبارة: " الطاقة الكامنة الثقالية معرفة بتقريب ثابت " أنه لا يمكن حسابها إلا إذا اخترنا وضعا مرجعيا، أي أن.

$$E_{pp}=mgh+E_{p{p}_0}$$

حيث: E_pp0 = Cte

حل التمرين الثالث حول الطاقة الكامنة صفحة 86

في الجملة (الجسم)، الجسم ليس له طاقة كامنة ثقالية.

حل التمرين الرابع حول الطاقة الكامنة صفحة 86

1/ حساب الطاقة الكامنة الثقالية:

نعتبر أن المستوي الذي وضعت عليه الأجورة هو المستوي المرجعي، وحيث أن مركز ثقل الأجورة يبعد عن هذا المستوي بالمسافة h = 10/2 = 5 cm

لدينا: E_pp = Mgh

حيث أن مركز ثقل الأجورة يبعد عن المستوي المرجعي بالمسافة h = 10/2 = 5 cm

ومنه نجد: E_pp1 = 2,4×9,80×5×10^-2 = 1,17 J

2- بنفس الطريقة نجد:

E_pp2 = 2,4×9,80×15×10^-2 = 3,53 J

3- استنتاج التغير في طاقتها الكامنة الثقالية:

ΔE = E_pp2 – E_pp1 = 2,36 J

حل التمرين الخامس حول الطاقة الكامنة صفحة 86

1 ـ تمثيل الحصيلة الطاقوية للجملة (الصندوق + الارض) بين الموضعين A و B:

باعتبار المستوي AD كمرجع لقياس الطاقة الكامنة الثقالية نجد:

2 ـ معادلة انحفاظ الطاقة:

$$E_{p{p}_A}+W_{AB}(\vec{F})=E_{p{p}_B}$$

3 ـ حساب عمل القوة:

لدينا:

$$W_{AB}(\vec{F}) = E_{pp_B} - E_{pp_A} = Mg(h_B - h_A)$$

ومنه:

$$W_{AB}(\vec{F}) = 29400 \, \text{J}$$

4 ـ يكون عمل القوة معدوم لأن شعاع القوة عمودي على شعاع الانتقال.

5 ـ عمل القوة من C إلى D هو نفس عملها من A إلى B لكن بإشارة مختلفة.

6 -عمل القوة من A إلى D معدوم.

حل التمرين السادس حول الطاقة الكامنة صفحة 87

1 ـ نعتبر الوضع المرجعي المستوي الأفقي المار من النقطة B، في الوضع A تملك الجملة (الكرية + الأرض) طاقة كامنة ثقالية E_ppA، لأنها توجد على ارتفاع h_o عن الوضع المرجعي.

2 ـ في الوضع B تكتسب الكرية طاقة حركية E_CB.

3 ـ إذا وصلت الكرية إلى النقطة C، فهذا يعني أن الجملة (الكرية + الأرض) معزولة طاقويا.

حل التمرين السابع حول الطاقة الكامنة صفحة 87

1 ـ حساب الطاقة الكامنة الثقالية للجملة في كل حالة:

نعتبر أن المصعد نقطة مادية. 

أ) الوضع المرجعي هو الطابق الأرضي (سطح الأرض):

z₁ = 9×3 = 27 m

E_pp1 = Mgz₁= 1025×9,8×27 = 271215 J

ب) الوضع المرجعي هو الطابق التاسع:

 z₂ = 0

E_pp2 = Mgz₂= 1025×9,8×0 = 0

ج) الوضع المرجعي هو الطابق العاشر:

z₃ = - 3 m

E_pp3 = Mgz₃= 1025×9,8×(- 3) = - 30135 J

2 ـ حساب عمل القوة المطبقة من طرف الكابل:

بما أن سرعة المصعد ثابته، والمسار مستقيم فان الحركة مستقيمة منتظمة، 

ومنه نجد: T = P

ومنه:

$$W(\vec{T})=W(\vec{P})=271215\text{J}$$

3 ـ حساب استطاعة القوة:

لدينا:

$$P=\frac{W(\vec{T})}{t}=\frac{W(\vec{P})}{t}=\frac{T\cdot z_1}{t}=T\cdot v$$

ومنه: P = 1025×9,8×1,2 = 12054 w

حل التمرين الثامن حول الطاقة الكامنة صفحة 87

نعتبر الجملة (الكرة + الأرض) معزولة طاقويا، أي نهمل مقاومة الهواء.

1 ـ حساب الطاقة الكامنة الثقالية للكرة عند مغادرتها يد الطفل:

E_ppA = mgz_A= 0,4×9,8×1,2 = 4,7 J

2 ـ ايجاد أقصى ارتفاع تبلغه الكرة:

بتطبيق مبدأ انحفاظ الطاقة للجملة (الكرة + الارض) بين الموضعين A و B:

E_CA + E_ppA = E_CB + E_ppB

عند أقصى ارتفاع تنعدم سرعة الكرة ومنه: E_CB = 0

ومنه: E_CA + E_ppA = E_ppB

ومنه: ½.mv_A² + mgz_A = mgz_B

ومنه: v_A² + 2gz_A = 2gz_B

ومنه:

$$z_B=\frac{2g{z}_A+v_A^2}{2g}=\frac{2\times \mathrm{9,8}\times \mathrm{1,2}+16}{2\times \mathrm{9,8}}=2\text{m}$$

3 ـ لتكن v_C سرعة الكرة عند النقطة C عند نزولها. (النقطة C منطبقة على النقطة A).

بتطبيق مبدأ انحفاظ الطاقة للجملة (الكرة) بين الموضعين A وC:

$$E_{C_A}+W_{AB}(\vec{P})+W_{BC}(\vec{P})=E_{C_C}$$

ومنه: E_CA - mg.AB + mg.BC = E_CC حيث: AB = BC

ومنه نجد: E_CA = E_CC 

ومنه:  v_A = v_C ومنه:

$${\vec{v}}_C=-{\vec{v}}_A$$

تعيين خصائص شعاع السرعة عند النقطة C:

المبدأ: النقطة C

الحامل: الشاقول الذي يشمل C

الجهة: نحو الاسفل

الطويلة: v_C = 4 m/s

4 ـ حساب سرعة الكرة لحظة ملامستها لسطح الارض:

الطريقة الاولى:

بتطبيق مبدأ انحفاظ الطاقة للجملة (الكرة) بين الموضعين C وO:

لدينا:
$E_{C_C} + W_{CO}(\vec{P}) = E_{C_O}$
ومنه:
$E_{C_C} + mg \cdot CO = E_{C_O}$
ومنه:
$\frac{1}{2}mv_C^2 + mg \cdot CO = \frac{1}{2}mv_O^2$
ومنه:
$v_O = \sqrt{2g \cdot CO + v_C^2}$

$v_O=\sqrt{2\times \mathrm{9,8}\times \mathrm{1,2}+16}=\mathrm{6,3}m\cdot s^{-1}$

الطريقة الثانية:

بتطبيق مبدأ انحفاظ الطاقة للجملة (الكرة + الارض) بين الموضعين C وO:

E_CC + E_ppC = E_CO + E_ppO حيث: E_ppO = 0

ومنه: E_CO = E_CC + E_ppC

ومنه: ½.mv_O² = ½.mv_C² + mgz_C

ومنه:

$$v_0 = \sqrt{2g \cdot z_C + v_C^2}$$$$v_0=\sqrt{2\times \mathrm{9,8}\times \mathrm{1,2}+16}=\mathrm{6,3}\text{ m/s}$$

حل التمرين التاسع حول الطاقة الكامنة صفحة 87

1 ـ حساب سرعة الكرية عند الوضع B:

بتطبيق مبدأ انحفاظ الطاقة على الجملة (الكرية + الارض)، بين الموضعين A وB:

نجد: E_CA + E_ppA = E_CB + E_ppB

نأخذ المستوي الافقي الذي يشمل النقطة B كمرجع لقياس الطاقة الكامنة الثقالية،

ومنه: E_ppB = 0 ولدينا: E_CA = 0  ومنه: E_ppA = E_CB

ومنه: mgh₁ = ½m.v_B² ومنه: v_B² = 2gh₁ ومنه: v_B = 1,98 m/s

2 ـ حساب سرعة الكرية عند الوضع C:

بتطبيق مبدأ انحفاظ الطاقة على الجملة (الكرية + الارض) بين الموضعين B وC:

نجد: E_CB + E_ppB = E_CC + E_ppC

نأخذ المستوي الافقي الذي يشمل النقطة C كمرجع لقياس الطاقة الكامنة الثقالية،

ومنه: E_ppC = 0 ومنه : E_CB + E_ppB = E_CC

ومنه: ½m.v_B² + mgh₂ = ½m.v_C²  ومنه: v_B² + 2gh₂ = v_C²

ومنه:

$$v_C = \sqrt{2g \cdot h_2 + v_B^2}$$$$v_C=\sqrt{2\times \mathrm{9,8}\times \mathrm{0,9}+\mathrm{3,92}}=\mathrm{4,64}\text{ m/s}$$

3 ـ حساب المدى X:

X = v_B.t = 1,98×0,5 = 1 m

حل التمرين العاشر حول الطاقة الكامنة صفحة 88

1 ـ حساب سرعة المتزحلق في النقطة B:

بتطبيق مبدأ انحفاظ الطاقة على الجملة (المتزحلق + الارض) بين الموضعين A وB:

نجد: E_CA + E_ppA = E_CB + E_ppB

نأخذ المستوي الافقي الذي يشمل النقطة B كمرجع لقياس الطاقة الكامنة الثقالية،

ومنه: E_ppB = 0 و لدينا : E_CA = 0  ومنه: E_ppA = E_CB

ومنه: Mgh = ½M.v_B² ومنه : v_B² = 2gh

ولدينا: h = AB.sinα ومنه : v_B² = 2g.AB.sinα

ومنه:

$$v_B = \sqrt{2g \cdot AB \cdot \sin(\alpha)}$$

ومنه:

$$v_B=\sqrt{2\times \mathrm{9,8}\times 100\times \mathrm{0,173}}=\mathrm{18,41}\text{m/s}$$

2 ـ حساب شدة قوة الاحتكاك:

بتطبيق مبدأ انحفاظ الطاقة على الجملة (المتزحلق + الارض) بين الموضعين A وB:

نجد: E_CA + E_ppA - |f.AB| = E_CB + E_ppB

نأخذ المستوي الافقي الذي يشمل النقطة B كمرجع لقياس الطاقة الكامنة الثقالية،

ومنه: E_ppB = 0 ولدينا: E_CA = 0  ومنه:E_ppA - |f.AB| = E_CB  

ومنه:

Mgh - |f.AB|  = ½M.v'_B²

ومنه:

Mg.AB.sinα - |f.AB|  = ½M.v'_B²

ومنه:

Mg.AB.sinα  = ½M.v'_B² + |f.AB| 

ومنه:

$$f = \frac{M \cdot g \cdot AB \cdot \sin(\alpha) - \frac{1}{2} M \cdot (v'_B)^2}{AB}$$

ولدينا:

$$v'_B = \frac{2v_B}{3} = \frac{2 \times 18{,}41}{3} = 12{,}27 \, \text{m/s}$$

ومنه:

$$f = \frac{85 \times 9{,}8 \times 100 \times 0{,}173 - 0{,}5 \times 85 \times 150{,}55}{100}$$

وأخيرًا:

$$f=80\text{N}$$

3 ـ ايجاد موضع النقطة C:

بتطبيق مبدأ انحفاظ الطاقة على الجملة (المتزحلق + الارض) بين الموضعين B وC:

نجد: E_CB + E_ppB - |f.BC| = E_CC + E_ppC

نأخذ المستوي الافقي الذي يشمل النقطة B كمرجع لقياس الطاقة الكامنة الثقالية،

ومنه: E_ppB = E_ppC = 0  ولدينا E_CC = 0  ومنه: E_CB - |f.BC| = 0

ومنه:

½M.v'_B² - |f.BC|  = 0

ومنه:

½M.v'_B² = |f.BC|

ومنه:

M.v'_B² = 2|f.BC| ومنه : BC = M.v'_B²/2|f|

ومنه:  BC = 85×150,55/2×80 = 80 m

حل التمرين 11 حول الطاقة الكامنة صفحة 88

ـ عبارة الطاقة الكامنة المرونية تكتب على الشكل: E_pe = ½kx²

ـ نعم تتعلق الطاقة الكامنة المرونية لنابض بمقدار استطالته أو انضغاطه.

ـ يحسب مقدار الاستطالة بالنسبة لوضع النابض في حالته الطبيعية.

ـ التغير في الطاقة الكامنة المرونية، لا يتعلق بمرجع الدراسة.

ـ عندما ينضغط نابض فإن طاقته الكامنة المرونية تزداد.

ـ عندما يستطیل نابض فإن طاقته الكامنة المرونية تزداد.

ـ عبارة الطاقة الكامنة لنابض الفتل تكتب على الشكل: E_pe = ½Cθ²

ـ عندما نفتل بزاوية سلك فتل فإن طاقته الكامنة المرونية تزداد.

ـ عندما نضغط على نابض أو نفتل سلكا فإنه يكتسب طاقة. 

حل التمرين 12 حول الطاقة الكامنة صفحة 88

1 ـ تحديد الجملة المدروسة:

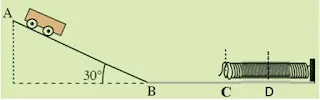
نختار الجملة (العربة + الأرض + النابض)، ونأخذ المستوي الافقي الذي يشمل النقطة B كمرجع لقياس الطاقة الكامنة الثقالية.

ومنه نجد:

عند النقطة A: لدينا طاقة كامنة ثقالية E_ppA

عند النقطة B: لدينا طاقة حركية E_CB

عند النقطة C: لدينا طاقة حركية E_CC

 عند النقطة D: لدينا طاقة كامنة مرونية E_peD

التحولات الطاقوية:

من A إلى B: تتحول الطاقة الكامنة الثقالية إلى طاقة حركية (تحويل ميكانيكي).

من B إلى C: لا يوجد تحول في الطاقة.

من C إلى D: تتحول الطاقة الحركية للعربة إلى طاقة كامنة مرونية في النابض (تحويل ميكانيكي).

2 ـ الحصيلة الطاقوية:

3 ـ معادلة انحفاظ الطاقة:

E_ppA + E_peC = E_ppB + E_peD حيث: E_peC = E_ppB = 0

ومنه: E_ppA = E_peD

4 ـ أقصى مسافة ينضغط بها النابض:

لدينا: E_ppA = E_peD

ومنه: Mgh = ½k.CD² حيث : βh = AB.sin ، CD = x

ومنه:

Mg.AB.sinβ = ½kx²  

ومنه:

2Mg.AB.sinβ = kx²

و لدينا: k = 4 N/cm = 400 N/m

ومنه:

$$x = \sqrt{\frac{2M \cdot g \cdot AB \cdot \sin(\beta)}{K}}$$

ومنه:

$$x = \sqrt{\frac{2 \times 0{,}8 \times 9{,}8 \times 0{,}8 \times 0{,}5}{400}}$$

وأخيرًا:

$$x=\mathrm{12,5}\text{cm}$$

5 ـ شدة القوة التي يطبقها النابض على العربة:

T = k.x = 400×0,125 = 50 N

6 ـ بما أن قوى الاحتكاك مهملة، فان العربة تصعد الى غاية النقطة A.