حول تمارين مقاربات الافعال المتبادلة الكهرومغناطيسية

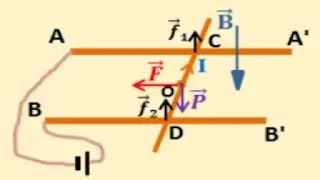
حل التمرين الأول صفحة 157:

1 ـ رسم شعاع القوة المطبقة على كل سلك:

2 ـ حساب قيمة القوة في كل حالة:

بالنسبة للحالة (a):

لدينا:

$$F = I \cdot l \cdot B \cdot \sin\theta$$

حيث: $\theta = 90^\circ$

ولدينا:

$$l = \frac{d}{\cos\alpha}$$

حيث: $\alpha = 30^\circ$

وبالتعويض:

$$F = \frac{I \cdot d \cdot B \cdot \sin\theta}{\cos\alpha}$$ $$F = \frac{5 \times 0,2 \times 40 \times 10^{-3} \times 1}{0,866}$$ $$F = 4,6 \times 10^{-2} \, \text{N}$$

بالنسبة للحالة (b):

لدينا:

$$F = I \cdot l \cdot B \cdot \sin\theta$$

حيث: $\theta = 90^\circ$

ولدينا:

$$l = \frac{d}{\cos\alpha}$$

حيث: $\alpha = 60^\circ$

وبالتعويض نجد:

$$F = \frac{I \cdot d \cdot B \cdot \sin\theta}{\cos\alpha}$$ $$F = \frac{5 \times 0,2 \times 40 \times 10^{-3} \times 1}{0,5}$$ $$F = 8,0 \times 10^{-2} \, \text{N}$$

بالنسبة للحالة (C):

لدينا:

$$F = I \cdot l \cdot B \cdot \sin\theta$$

حيث:
$\theta = 90^\circ$
وبذلك تصبح المعادلة:

$$F = I \cdot l \cdot B \cdot \sin(90^\circ)$$

وبما أن $\sin(90^\circ) = 1$، تصبح:

$$F = I \cdot l \cdot B$$

ومنه: F = 5×0,2×40×10^-3

ومنه: F = 4,0×10^-2 N

بالنسبة للحالة (d):

لدينا:

$$F = I \cdot l \cdot B \cdot \sin\theta$$

وبما أن:

$$l = 2d$$

وبالتعويض نجد:

$$F = I \cdot (2d) \cdot B \cdot \sin\theta$$

وبما أن $\theta = 90^\circ$ و $\sin 90^\circ = 1$، نحصل على:

$$F = 2I \cdot d \cdot B$$

ومنه: F = 2×5×0,2×40×10^-3

ومنه: F = 8,0×10^-2 N

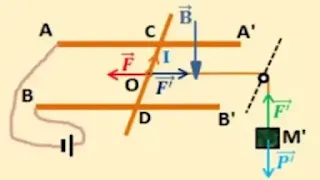
حل التمرين الثاني صفحة 157:

1 ـ تمثيل الحقل المغناطيسي في نقطة من القطعة MN:

2 ـ نعم يمكن القول أن القطعة MN خاضعة لحقل منتظم، لأن خطوط الحقل متوازية

3 ـ حساب القوة الكهرومغناطيسية التي تؤثر على القطعة المستقيمة:

لدينا:

$$F = I \cdot l \cdot B \cdot \sin\theta$$

وبما أن:

$$\theta = 90^\circ$$

وبما أن:

$$\sin 90^\circ = 1$$

تصبح المعادلة:

$$F = I \cdot l \cdot B$$

ومنه: F = 1×0,1×10×10^-6

ومنه: F = 10^-6 N

ـ تمثيل القوة الكهرومغناطيسية: (أنظر الصورة السابقة)

4 ـ عند عكس جهة التيار تنعكس جهة القوة.

5 ـ عند مضاعفة شدة التيار I₂ تتضاعف شدة القوة دون تغير شدتها.

حل التمرين الثالث صفحة 157:

1 ـ تمثيل الكابل و شعاع الحقل المغناطيسي الأرضي:

2 ـ إعطاء خصائص قوة لابلاس المطبقة على الكابل و الناتجة عن المركبة الأفقية للحقل المغناطيسي الأرضي:

المبدأ: في منتصف القطار

الحامل: شاقولي

الجهة: نحو الأعلى

الشدة (الطويلة):

لدينا:

$$F = I \cdot l \cdot B_h \cdot \sin\theta$$

ومنه: F = 1000×50×20×10^-6×sin25°

ومنه: F = 0,42 N

3 ـ إعطاء خصائص قوة لابلاس المطبقة على الكابل و الناتجة عن المركبة العمودية للحقل المغناطيسي الأرضي:

المبدأ: في منتصف القطار

الحامل: شاقولي

الجهة: كما في الشكل

الشدة (الطويلة):

لدينا:

$$F_v = I \cdot l \cdot B_v \cdot \sin\theta$$

حيث: $\theta = 90^\circ$، وبذلك تصبح:

$$F_v = I \cdot l \cdot B_v$$

لكن لدينا:

$$B_v = B_h \cdot \tan I$$

حيث: $I = 60^\circ$، وبالتعويض:

$$F_v = I \cdot l \cdot B_h \cdot \tan I \cdot \sin\theta$$

وبما أن $\sin 90^\circ = 1$، تصبح:

$$F_v=I\cdot l\cdot B_h\cdot \tan I$$

ومنه: F = 1000×50×20×10^-6×1,732×1

ومنه: F_v = 1,732 N

حل التمرين الرابع صفحة 157:

لدينا:

$$F_1 = I \cdot l \cdot B$$

بالتعويض نجد:

$$F_1 = 5 \times 2 \times 10^{-2} \times 10 \times 10^{-3}$$

ومنه: F₁ = 10^-3 N

ولدينا: F₂ = 0 N

ولدينا:

$$F_3 = I \cdot l \cdot B$$

بالتعويض نجد:

$$F_3 = 5 \times 2 \times 10^{-2} \times 10 \times 10^{-3}$$

ومنه: F₃ = 10^-3 N

حل التمرين الخامس صفحة 158:

إيجاد الحالة التي ينزاح فيها الاطار عن وضع التوازن عند مرور التيار I من M نحو N:

1 ـ الحالة الأولى: لا تحدث إزاحة.

2 ـ الحالة الثانية: لا تحدث ازاحة.

3 ـ الحالة الثالثة: تحدث ازاحة.

حل التمرين السادس صفحة 158:

شرح لماذا تزداد القيمة المعطاة في الربيعة:

تزداد القيمة المعطاة في الربيعة بسبب نشوء قوة كهرومغناطيسية متجهة نحو الأسفل، كما يوضحه الشكل التالي:

1 ـ تعيين جهة الحقل المغناطيسي:

(أنظر الصورة السابقة)

2 ـ تمثيل القوى المؤثرة على الإطار:

(أنظر الصورة السابقة)

القوة المسببة لهذه الاستطالة هي القوة المتجهة نحو الأسفل، كما في الصورة السابقة

3 ـ إيجاد شدة الحقل المغناطيسي:

لدينا:

$$F = I \cdot l \cdot B \cdot \sin\theta$$

حيث: $\theta = 90^\circ$

وبترتيب المعادلة لإيجاد $B$:

$$B = \frac{F}{I \cdot l}$$

بالتعويض:

$$F = 2,7 - 2,4 = 0,3 \, \text{N}$$ومنه:
$$B = \frac{0,3}{0,5 \times 0,04}$$ $$B = 15 \, \text{T}$$

4 ـ عند تغيير جهة التيار تتغير اشارة الربيعة من 2,4 N الى 2,1 N

حل التمرين السابع صفحة 158:

أ ـ تعيين القوى المؤثرة على القضيب DC:

ب ـ لا يمكن للقضيب أن يكون متوازنا في هذه الظروف، لأن القوى لا تفني بعضها البعض، أي أن المجموع الشعاعي للقوى المؤثرة على القضيب لا يساوي الشعاع المعدوم.

ج ـ يجب تطبيق قوة مساوية للقوة F ، ومعاكسة لها في الجهة.

د ـ تعيين خصائص القوة المطبقة في O من طرف الخيط على القضيب:

المبدأ: النقطة O

الحامل: كما في الشكل

الجهة: كما في الشكل

الشدة: عند التوازن نجد: F' = P' = M'.g

ومنه: F' = 15×10^-3×9,8 = 0,147 N

و لدينا:

$$F = I \cdot l \cdot B$$

بالتعويض نجد:

$$F = 5 \times 8 \times 10^{-2} \times 0,5$$ومنه:
$$F = 0,2 \, \text{N}$$

نلاحظ أن F ˃ F' ومنه فالقضيب لا يتوازن بحيث تكون محصلة القوى في جهة القوة F

هـ ـ حساب عمل ثقل الجسم خلال صعوده:

W = - P'.h = - 0,147×0.2

ومنه: W = - 2,94×10^-2 J

حساب عمل قوة لابلاس خلال الحركة:

W' = F.d = 0,2×0,2  ومنه: W' = 4×10^-2 J

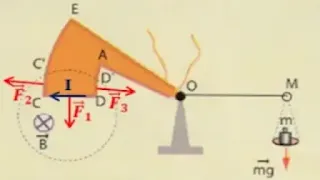
حل التمرين الثامن صفحة 159:

أ ـ القوتان F₂ ، F₃ لا تتدخلان في اختلال التوازن، لأن حاملهما يلاقي محور الدوران، أي ليس لهما عزم 

ب ـ خصائص القوة المؤثرة على القطعة CD:

المبدأ: منتصف القطعة CD

الحامل: شاقولي

الجهة: نحو الأسفل

الشدة: F = I.a.B

ج ـ حساب قيمة الحقل المغناطيسي:

لدينا: F = I.a.B ، ولدينا: F = mg ومنه نجد: I.a.B = mg 

ومنه:

$$B = \frac{mg}{I \cdot a}$$

بالتعويض نجد:

$$B = \frac{0,6 \times 10^{-3} \times 9,8}{3 \times 2 \times 10^{-2}}$$ $$B=0,098\text{T}$$