حلول تمارين الكتاب المدرسي حول العمل والطاقة الحركية

حل التمرين الأول حول العمل و الطاقة الحركية صفحة 46

اختيار الجواب الصحيح:

ـ عبارة عمل قوة شدتها ثابتة هي:

أ/ W = F.d (صحيح في حالة خاصة)

ب/ 

W = F.d.sinα (خطأ)

ج/

W = F.d.cosα (صحيح)

د/ 

W = F.d.α (خطأ)

ـ عمل هذه القوة هو

W = F.d = 3×10 = 30 J

يحسب عمل الثقل بالعلاقة: W = P(h_A – h_B)

ـ نعبر عن الاستطاعة بالعلاقة:

  P = W/Δt

ـ اذا كانت الزاوية 90°

ـ لا يتعلق بالمسار المتبع

حل التمرين الثاني حول العمل و الطاقة الحركية صفحة 46

تصحيح التصريحات الخاطئة:

1 ـ عمل قوة ثابتة يساوي دائما 

F.d.cosα

3 ـ عمل قوة الاحتكاك  – f.d

حل التمرين الثالث حول العمل و الطاقة الحركية صفحة 46

بما أن مجال الجاذبية الأرضية غير ثابت و يتغير بدلالة الارتفاع عن سطح الأرض حيث أن الثقل يكون ثابت من أجل الارتفاعات الصغيرة فقط ، نستنتج أن تطبيق هذه العلاقة غير صحيح .

حل التمرين الرابع حول العمل و الطاقة الحركية صفحة 46

1. لدينا:

$$\cos \alpha = \frac{W}{F \cdot d} = \frac{125}{10.27 \times 13} = 0.936$$

وبالتالي:

$$\alpha = \arccos(0.936) \approx 20.6^\circ$$

2. لدينا:

$$\cos \alpha =\frac{W}{F\cdot d}=\frac{134}{10.27\times 13}=1$$

نعم يمكن أن يكون العمل مساويا للقيمة 134 J لأن

cosα = 1

حل التمرين الخامس حول العمل و الطاقة الحركية صفحة 47

أ/  W = F.d = 6×1,52 = 9,12 J

ب/  W = F.d.cosα = 16×21,52cos28 = 304 J

ج/  W = F.d.cosα = 12,3×11,50cos125 = - 81,13 J

حل التمرين السادس حول العمل و الطاقة الحركية صفحة 47

• لدينا:

$$W_{AB}(\vec{F}) = F \cdot d \cdot \cos \alpha$$

• الحالة الأولى:

$$W_{AB}(\vec{F}) = 10 \times 10 = 100 \, \text{J}$$

• الحالة الثانية:

$$W_{AB}(\vec{F}) = 10 \times 11.6 \times 0.86 = 100 \, \text{J}$$

• الحالة الثالثة:

$$W_{AB}(\vec{F})=10\times 20\times 0.5=100\text{J}$$

نلاحظ أن قيمة العمل ثابتة، ونستنتج أن العمل يتناسب طرديا مع الانتقال وعكسيا مع الزاوية α، بحيث α تنتمي الى المجال [0 ; π/2]

حل التمرين السابع حول العمل و الطاقة الحركية صفحة 47

• لدينا:

$$F = \frac{W_{AB}(\vec{F})}{AB \cdot \cos \alpha}$$

• الحالة الأولى (من أجل $\alpha = 0^\circ$):

$$F = \frac{100}{10 \cdot 1} = 10 \, \text{N}$$

• الحالة الثانية (من أجل $\alpha = 30^\circ$):

$$F = \frac{100}{10 \cdot 0.86} = 11.6 \, \text{N}$$

• الحالة الثالثة (من أجل $\alpha = 60^\circ$):

$$F=\frac{100}{10\cdot 0.5}=20\text{N}$$

كلما زادت الزاوية α بحيث α تنتمي الى المجال [0 ; π/2] يجب أن نبذل قوة أكبر لكي نحصل على نفس العمل في نفس الانتقال .

حل التمرين التاسع حول العمل و الطاقة الحركية صفحة 47

1) عند رفع الجسم شاقوليا:

الطريقة الأولى:

بما أن سرعة الجسم ثابتة فإن الجملة (جسم) تحقق مبدأ العطالة، أي أن:

• لدينا:

$$\vec{F} + \vec{P} = \vec{0} \quad \rightarrow \quad (1)$$

• بإسقاط العبارة (1) على محور الحركة نجد:

$$F = P$$

• ومنه:

$$W_{AB}(\vec{F}) = \left| W_{AB}(\vec{P}) \right| = |P \cdot h|$$

• تطبيق عددي:

$$W_{AB}(\vec{F})=980\times 10=9.8\times 10^3\text{J}$$

الطريقة الثانية:

• نكتب معادلة انحفاظ الطاقة للجملة (الجسم):

$$E_{C_A} + W_{AB}(\vec{F}) - \left| W_{AB}(\vec{P}) \right| = E_{C_B}$$

• حيث:

$$E_{C_A} = E_{C_B}$$

• ومنه نجد:

$$W_{AB}(\vec{F}) = \left| W_{AB}(\vec{P}) \right| = 9.8 \times 10^3 \, \text{J}$$

2) عند سحب الجسم على طريق أفقي:

الطريقة الأولى:

بما أن سرعة الجسم ثابتة فإن الجملة (جسم) تحقق مبدأ العطالة:

• أي أن:

$$\vec{F} + \vec{P} + \vec{R} + \vec{f} = \vec{0} \quad \rightarrow \quad (1)$$

• بإسقاط العبارة (1) على محور الحركة نجد:

$$F = f$$

• ومنه:

$$W_{AB}(\vec{F}) = \left| W_{AB}(\vec{f}) \right|$$

• ومنه:

$$W_{AB}(\vec{F}) = 300 \times 10 = 3.0 \times 10^3 \, \text{J}$$

الطريقة الثانية:

نكتب معادلة انحفاظ الطاقة للجملة (جسم)

• نجد:

$$E_{C_A} + W_{AB}(\vec{F}) - \left| W_{AB}(\vec{f}) \right| = E_{C_B}$$

• حيث:

$$E_{C_A} = E_{C_B}$$

• ومنه:

$$W_{AB}(\vec{P}) = W_{AB}(\vec{R}) = 0$$

• ومنه نجد:

$$W_{AB}(\vec{F}) = \left| W_{AB}(\vec{f}) \right| = 3.0 \times 10^3 \, \text{J}$$

3) عند سحب الجسم نحو الاعلى على مستوي مائل:

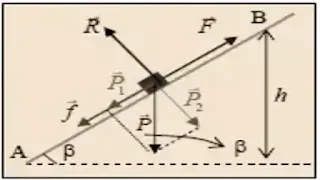
الطريقة الأولى:

بما أن سرعة الجسم ثابتة فإن الجملة (جسم) تحقق مبدأ العطالة:

• أي أن:

$$\vec{F} + \vec{P} + \vec{R} + \vec{f} = \vec{0} \quad \rightarrow \quad (1)$$

• بإسقاط العبارة (1) على محور الحركة نجد:

$$F = f + P_1 = f + P \sin \beta$$

• التطبيق العددي:

$$F = 300 + \frac{980 \times 6}{10} = 888 \, \text{N}$$

• ولدينا:

$$W_{AB}(\vec{F}) = F \cdot AB \cdot \cos \alpha$$

• ومنه:

$$W_{AB}(\vec{F})=888\times 10\times 1=8880\text{J}$$

الطريقة الثانية:

نكتب معادلة انحفاظ الطاقة للجملة (جسم)

• نجد:

$$E_{C_A} + W_{AB}(\vec{F}) - \left| W_{AB}(\vec{P}) \right| - \left| W_{AB}(\vec{f}) \right| = E_{C_B}$$

• حيث:

$$E_{C_A} = E_{C_B}$$

• ومنه نجد:

$$W_{AB}(\vec{F}) = \left| W_{AB}(\vec{P}) \right| + \left| W_{AB}(\vec{f}) \right|$$

• ومنه:

$$W_{AB}(\vec{F}) = \left| W_{AB}(\vec{f}) \right| + \left| W_{AB}(\vec{P}) \right|$$

• ومنه:

$$W_{AB}(\vec{F}) = f \cdot AB + P \cdot h$$

• ومنه:

$$W_{AB}(\vec{F}) = 300 \times 10 + 980 \times 6 = 8880 \, \text{J}$$

• 4 ـ لدينا:

$$P = \frac{W_{AB}(\vec{F})}{\Delta t}$$

• التطبيق العددي:

$$P_1 = \frac{9.8 \times 10^3}{55} = 1.8 \times 10^2 \, \text{W}$$$$P_2 = \frac{3 \times 10^3}{55} = 54 \, \text{W}$$$$P_3=\frac{9.8\times 10^3}{55}=1.8\times 10^2\text{W}$$

حل التمرين العاشر حول العمل و الطاقة الحركية صفحة 48

تصحيح التصريحات الخاطئة :

ـ عندما تتضاعف سرعة جسم متحرك بحركة انسحابيه ، أي عندما تضرب السرعة في 2 فإن الطاقة الحركية تضرب في 4 .

ـ إذا أثرت قوة على جسم فإن طاقته الحركية تتغير إذا تغيرت سرعته بفعل هذه القوة .

- إذا كان جسم يتحرك بسرعة ثابتة فإن مجموع أعمال كل القوى المؤثرة عليه يكون معدوما (هذا لا يعني أن عمل كل قوة يكون معدوما)

حل التمرين 11 حول العمل و الطاقة الحركية صفحة 48

اختيار الجواب الصحيح :

الجواب الصحيح هو (ب)، أي  E_C2 = 2E_C1

• عند الصعود تتغير الطاقة الحركية للجسم من E_C1 إلى E'_C1 حيث E'_C1 = 0 (لأن الجسم يتوقف لكي يرجع).

عند الصعود:

E'_C1 – E_C1 = -Ph → (1)

عند النزول:

E_C2 – E'_C1 = Ph → (2)

بجمع العلاقتين (1) و (2) نجد E_C2 = E_C1

حل التمرين 12 حول العمل و الطاقة الحركية صفحة 48

الجسم	الكتلة	السرعة	الطاقة الحركية
حركة إلكترون في الأنبوب المهبطي للتلفاز	9,1× 10-31 kg	2×106 m/s	18,20×10-19 J
حركة كرة القدم	0,400 kg	14 m/s	39,2 J
سيارة في الطريق السريع	1400 kg	22,2 m/s	3,45 × 105 J
طائرة عند الإقلاع	75000 kg	69,4 m/s	1,80×108 J
دراج ودراجته في مسابقة رياضية	90 kg	11,1 m/s	5,54 × 103J
رصاصة تنطلق من مسدس	0,005 kg	800 m/s	1,6 × 103J

حل التمرين 13 حول العمل و الطاقة الحركية صفحة 48

1/ لدينا: E_C = ½Mv²

    ولدينا : M = 1,2 × 1000 = 1200 kg

ـ من أجل v = 120 km/h = 120/3,6 = 33,3m/s 

     تكون الطاقة الحركية:

  E_C = ½×1200×(33,3)²   ومنه: E_C = 6,65×10⁵ J

ـ من أجل v = 120 km/h = 80/3,6 = 22,2m/s 

     تكون الطاقة الحركية:

  E_C = ½×1200×(22,2)²  ومنه: E_C = 2,95×10⁵ J

ـ من أجل v = 120 km/h = 40/3,6 = 11,1m/s 

تكون الطاقة الحركية:

  E_C = ½×1200×(11,1)²  ومنه : E_C = 7,65×10⁴ J

2 - الارتفاعات الموافقة:

• لدينا:

$$E_{C_0} + W(\vec{P}) = E_C$$

ومنه: Ph = E_C – E_C0 حيث E_C0 = 0 و  P = Mg

ومنه: h = E_C/Mg

ومنه نجد:

$$h_1 = \frac{6.65 \times 10^5}{1200 \times 9.8} = 56.5 \, \text{m}$$$$h_2 = \frac{2.95 \times 10^5}{1200 \times 9.8} = 25.1 \, \text{m}$$$$h_3 = \frac{7.65 \times 10^4}{1200 \times 9.8} = 6.5 \, \text{m}$$

حل التمرين 14 حول العمل و الطاقة الحركية صفحة 48

• 1/ لدينا:

$$E_{C_1}+W(\vec{P})=E_{C_2}$$

حيث E_C1 = 0 و  P = Mg ومنه: E_C2 = Mgh

ومنه: E_C2 = 60×9,8×40 = 23520 J

2/ لدينا: E_C = ½Mv² ومنه:

$$v=\sqrt{\frac{2E_{C_2}}{M}}=\sqrt{\frac{2\times 23520}{60}}$$

ومنه: v = 28 m/s

حل التمرين 16 حول العمل و الطاقة الحركية صفحة 49

1 ـ حساب التغير في الطاقة الحركية للطائرة بين لحظتي الانطلاق و الاقلاع:

لدينا: ΔE_C = E_C2 – E_C1 = ½Mv² ( لأن E_C1 = 0 )

ومنه:

$$\Delta E_C = 0.5 \times 70 \times 10^3 \times \left( \frac{300}{3.6} \right)^2$$

ومنه:

$$\Delta E_C = 0.5 \times 70 \times 10^3 \times (83.33)^2$$ومنه:
$$\mathrm{\Delta }{E}_C=2.43\times 10^8\text{J}$$

2 ـ حساب عمل القوة المحركة الموافقة:

W = F.d = 3,5×10⁵×900 = 3,15×10⁸ J

3 ـ مقارنة قيمتي العمل و التغير في الطاقة الحركية:

نلاحظ أن العمل المنجز أكبر من التغير في الطاقة الحركية، ومنه نستنتج أنها توجد احتكاكات

4 ـ تمثيل الحصيلة الطاقوية للطائرة بين لحظتي الانطلاق و الاقلاع:

حل التمرين 17 حول العمل و الطاقة الحركية صفحة 49

حساب الطاقة الحركية لواحد متر مكعب من الهواء:

نحسب كتلة واحد متر مكعب من الهواء

M = ρ.V = 1,293×1000 = 1293 g = 1,293 kg

من أجل v = 50km/h = 13,89 m/s 

نجد: E_C = ½Mv² = 0,5×1,293×(13,89)² = 124,7 J

من أجل v = 100 km/h = 27,78 m/s 

نجد: E_C = ½Mv² = 0,5×1,293×(27,78)² = 498,92 J

حل التمرين 18 حول العمل و الطاقة الحركية صفحة 49

1/ ايجاد عبارة عمل الثقل بدلالة الزاويتين α و β:

لدينا: W = Ph

ولدينا: h = h₂ – h₁

ولدينا: h₁ = Rcosα ، h₂ = Rcosβ

ومنه: h = Rcosβ – Rcosα ومنه : h = R(cosβ –cosα)

ومنه: W = P.R(cosβ –cosα)

2/ ايجاد عبارة الطاقة الحركية للكرة في الموضع B:

$$E_{C_A}+W(\vec{P})=E_B$$

ومنه: E_CB = E_CA + P.R(cosβ –cosα)

ملاحظة: عمل قوة رد الفعل معدوم لان شعاعه عمودي على شعاع الانتقال في كل لحظة.

حل التمرين 19 حول العمل و الطاقة الحركية صفحة 49

1/ حساب عمل الثقل من النقطة A الى النقطة B:

W = Ph = 25×1,8 = 45 J

2/ تمثيل الحصيلة الطاقوية للجملة (الكرة) بين A و B:

3/ معادلة انحفاظ الطاقة للجملة (الكرة):

$$E_{C_A} + W(\vec{P}) = E_B$$

أو:

$$\Delta E_C = W(\vec{P})$$

وأيضًا:

$$W=\mathrm{\Delta }{E}_C=E_{C_B}-E_{C_A}$$

4/ استنتاج سرعة الكرة عند B:

من معادلة انحفاظ الطاقة نجد:

½Mv_B² = Mgh + ½Mv_A²

ومنه: v_B² = 2gh + v_A²  ومنه:

$$v_B = \sqrt{v_A^2 + 2gh}$$

ومنه نجد:

v_B = 11,63 m/s

حل التمرين 20 حول العمل و الطاقة الحركية صفحة 49

ايجاد سرعة الكرة لحظة لمسها الارض:

لدينا:

$$E_{C_A}+W_{AB}(\vec{P})+W_{BA}(\vec{P})+W_{AO}(\vec{P})=E_{C_O}$$

ومنه: ½Mv_A² – P.AB + P.AB + P.AO = ½Mv_O²

ومنه: v_O² = 2gh + v_A²  ومنه:

$$v_O = \sqrt{v_A^2 + 2gh}$$

ونجد:

v_O = 7,71 m/s

حل التمرين 21 حول العمل و الطاقة الحركية صفحة 49

1/ حساب سرعة المتزحلق عندما يقطع مسافة قدرها 40 m:

لدينا:

$$E_{C_A}+W_{AB}(\vec{P})+W_{AB}(\vec{R})=E_{C_B}$$

ومنه: ½Mv_A² – P.h + 0 = ½Mv_B²

ولدينا: h = AB.sinα 

ومنه: ½Mv_A² – M.g. AB.sinα = ½Mv_B²

ومنه: v_A² – 2.g. AB.sinα = v_B²  ومنه:

$$v_B = \sqrt{v_A^2 - 2g \cdot AB \cdot \sin \alpha}$$

• التطبيق العددي:

$$v_B=\sqrt{21^2-2\times 9.8\times 40\times \sin 20^{\circ }}$$

ومنه:

v_B = 13,15 m/s

2/ ايجاد المسافة المقطوعة عندما تنعدم سرعته:

نعتبر ان المتزحلق يتوقف عند نقطة C ومنه نجد:

v_A² – 2.g. AC.sinα = v_C² حيث v_C = 0

ومنه: AC = v_A²/2.g.sin20°

ومنه:

$$AC = \frac{441}{2 \times 9.8 \times 0.34}$$

ومنه:

$$AC = \frac{441}{6.664} \approx 66.17 \, \text{m}$$

3/ حساب الاحتكاكات المطبقة على المتزلج من طرف الارضية:

نعتبر ان المتزحلق يتوقف عند نقطة D ومنه نجد: 

نكتب معادلة انحفاظ الطاقة للجملة (متزحلق)

$$E_{C_A}+W_{AD}(\vec{P})+W_{BD}(\vec{R})+W_{AD}(\vec{f})=E_{C_D}$$

ومنه: 

½Mv_A² – M.g.h + 0 - f.AD = ½Mv_D² → (1)

ولدينا:

$$v_D = 0$$

و:

$$AD = \frac{3 \times AC}{5}$$

ومنه:

$$AD = \frac{3 \times 66.17}{5} = \frac{198.51}{5} = 39.70 \, \text{m}$$

 h = AD.sin20° = 39,70×0,34 = 13,5 m

بالتعويض في العلاقة (1) نجد:

0,5×80×441 - 80×9,8×13,5 – 39,70f  = 0

ومنه: f  = 177,73 N

حل التمرين 22 حول العمل و الطاقة الحركية صفحة 50

1/ تمثيل القوى المطبقة على السيارة:

2/ حساب مجموع أعمال القوى المطبقة على السيارة عندما تتحرك من السكون من A إلى B:

\[ W_m = W_{AB}(\vec{F}) + W_{AB}(\vec{F'}) + W_{AB}(\vec{P}) + W_{AB}(\vec{R}) + W_{AB}(\vec{f}) \]

ومنه:

W_m = F.AB.cosα + F'.AB + 0 + 0 – f.AB

ومنه:

W_m = 880×40×0,86 + 310×40 - 270×40

ومنه:

W_m = 31872 J

3/ تمثيل الحصيلة الطاقوية للجملة (سيارة) بين الموضعين A و B:

4/ ايجاد سرعة السيارة في الوضع B:

بتطبيق مبدأ انحفاظ الطاقة للجملة (سيارة) بين الموضعين A و B نجد:

E_CA + W_m = E_CB حيث: E_CA = 0 

ومنه: E_CB = ½Mv_B² = W_m

ومنه: v_B² = 2W_m/M 

ومنه: v_B = 8,41 m/s