الاختبار الثاني في مادة الفيزياء للسنة الثالثة ثانوي 2025/2024

يعد الاختبار الثاني في مادة الفيزياء، محطة تقييمية هامة لتلاميذ السنة الثالثة ثانوي، خلال الموسم الدراسي 2024-2025. يهدف إلى قياس مدى استيعاب التلاميذ للمفاهيم العلمية المدروسة، مثل الظواهر الكهرباء، تطور جملة كيميائية نحو حالة التوازن، والتحولات النووية، وفقًا للبرنامج الرسمي المعتمد.

يُجرى الاختبار في ظروف رسمية، مع التركيز على تحليل المسائل، حل التمارين، واستخدام القوانين الفيزيائية بشكل دقيق. يُنصح التلاميذ بالتحضير الجيد من خلال مراجعة الدروس، حل التمارين التطبيقية، والاطلاع على الاختبارات السابقة لاكتساب مهارات التفكير العلمي والمنهجي.

ملاحظة : يوجد الاختبار مع الحل بصيغة الـ PDF في نهاية المقال

التمرين الأول:(07 نقاط)

كل القياسات مأخوذة في درجة الحرارة 25°C.

I ـ حضرنا محلول (S₀) لمحلول حمض الايثانويك CH₃COOH_(aq)))، تركيزه المولي C₀ = 0,1 mol/L . بإذابة كتلة m من الايثانويك النقي في حجم V = 100mL من الماء المقطر، نقيس قيمة الـ pH له نجد 2,9

1 ـ أ ـ جد قيمة الكتلة m ؟

   ب ـ اذكر البروتوكول التجريبي لتحضير المحلول (S₀) ؟

2 ـ أ ـ اكتب معادلة التفاعل المنمذج للتحول الكيميائي بين حمض الايثانويك والماء؟

   ب ـ هل التفاعل السابق تم بين حمض وأساسه المرافق، أو حمض الثنائية وأساس لثنائية أخرى؟

3 ـ أ ـ انشئ جدول تقدم التفاعل؟

   ب ـ احسب قيمة نسبة التقدم النهائي للتفاعل τ_f ، ماذا تستنتج؟

   جـ ـ احسب قيمة ثابت التوازن K للتفاعل؟

 يعطى:M(CH₃COOH) = 60 g/mol

II ـ انطلاقا من المحلول السابق (S₀) نحضر محاليل (S_i) ممددة، وذلك بأخذ في كل مرة حجما V₀ = 10 mL من المحلول الأصلي (S₀) ونضيف له حجماً مناسباً من الماء المقطر \( V_{\text{H}_2O} \).

وعند حدوث التوازن الكيميائي للمحاليل (S_i) المحضرة نقوم بقياس الـ pH لكل محلول فنحصل على النتائج المدونة في الجدول التالي:

المحاليل (Si)	(S1)	(S2)	(S3)	(S4)	(S5)	(S6)
\( V_{\text{H}_2O} \) (mL)	0	10	20	40	60	90
pH	2,9	3,05	3,15	3,25	3,30	3,40
C(mol/L)
- log(C)

1 ـ أ ـ اكتب عبارة التركيز المولي C للمحاليل (S_i) بدلالة C₀ و V₀ و ؟

   ب ـ اكمل الجدول؟

   جـ ـ اذكر الخطوات العملية لتحضير المحلول (S₃) ؟

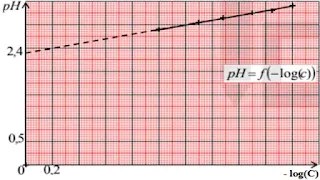
2 ـ أ ـ اعتمادا على سلم رسم مناسب، ارسم البيان pH = f(-log(c)) ؟

   ب ـ اكتب المعادلة الرياضية للبيان ؟

3 ـ أ ـ جد العلاقة النظرية بين pH و pK_a للثنائية CH₃COOH_(aq)/CH₃COO^-_(aq))) ؟

   ب ـ بإهمال [CH₃COO^-] أمام C بين أن: pK_a = 2pH +log(C) ؟

4 ـ استنتج قيمة pK_a للثنائية CH₃COOH_(aq)/CH₃COO^-_(aq))) ؟

التمرين الثاني:(04,25 نقاط)

\( {}^{32}_{15}P \) إشعاعي النشاط \(\beta^-\) ، يوجد على شكل محلول ويستعمل في الطب لمعالجة داء الفاكيز (تكاثر غير طبيعي للكريات الحمراء في الدم) عبر الحقن الوريدي حيث يلتصق بشكل انتقائي على الكريات الحمراء للدم فيدمرها بسبب الإشعاع المنبعث منه.

معطيات:

• الكتلة المولية للفوسفور-32 هي: \( M({}^{32}_{15}P) = 32 \, \text{g.mol}^{-1} \).
• ثابت أفوقادرو: \( N_A = 6.02 \times 10^{23} \, \text{mol}^{-1} \).

مقتطف من الجدول الدوري للعناصر:

\( {}_{17}Cl \), \( {}_{16}S \), \( {}_{15}P \), \( {}_{14}Si \), \( {}_{13}Al \), \( {}_{12}Mg \).

1 ـ حدد الصفة أو الصفات التي تميز تفكك نواة مشعة معينة.

    (1): تلقائي ، (2): متوقع في الزمن ، (3): عشوائي ، (4): حتمي ، (5): يتعلق العوامل الخارجية

2 ـ أعط تعريف النظائر؟

3 ـ أعط تركيب نواة الفوسفور \(_{15}^{32}\text{P}\) ؟

4 ـ اكتب معادلة التفكك الموافقة لتحول نواة الفوسفور \(_{15}^{32}\)P محددا النواة الناتجة ؟

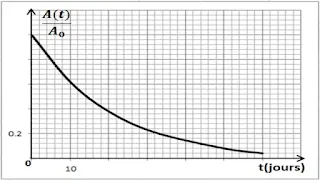
5 ـ يمثل المنحنى جانبه تغير النسبة $\frac{A(t)}{A_0}$ لعينة من الفوسفور 32 بدلالة الزمن. حدّد بالثانية (s)، زمن نصف العمر $t_{1/2}$ ثم استنتج قيمة ثابت التفكك الإشعاعي $\lambda$ ؟

6 ـ يعالج مريض مصاب بداء الفاكيز عن طريق الحقن الوريدي بمحلول فوسفات الصوديوم الذي يحتوي على كتلة $m_0 = 1,00 \times 10^{-8} \, \text{g}$ من الفوسفور 32.

   أ ـ احسب عدد الأنوية الابتدائية N₀ للفوسفور32 ؟

 ب ـ استنتج قيمة النشاط الإشعاعي A₀ للحقنة في اللحظة t₀ = 0 ؟

7 ـ ينعدم مفعول الدواء في جسم المريض عندما يصبح النشاط الإشعاعي A للحقنة مساويا للقيمة A = 1,05×10⁶ Bq . حدد، بالأيام (j)، المدة الزمنية اللازمة لانعدام مفعول الدواء؟

التمرين الثالث:(08,75 نقاط)

نحقق التركيب التجريبي المبين في الشكل (1) باستعمال التجهيز التالي:

* مولد ذي توتر ثابت E.

* مكثفة سعتها C غير مشحونة.

* ناقلين أوميين مقاومتهما R₁ = 1kΩ و R₂

* بادلة k وأسلاك توصيل.

I ـ نضع البادلة k في اللحظة t = 0 عند الوضع (1).

1 ـ مثل على الدارة المدروسة جهة كل من التيار الكهربائي i و مثل بالأسهم التوترين u_C و u_R

2 ـ أ ـ اكتب المعادلة التفاضلية لتطور شدة التيار i(t).

   ب ـ تحقق أن العبارة:

$$i(t)=\frac{E}{R_1}{e}^{-\frac{t}{{\tau }_1}}$$

حل للمعادلة التفاضلية، حيث:

$$\tau_1 = R_1 C$$

   ت ـ استنتج عبارة التوتر  بين طرفي الناقل الأومي R₁

   ث ـ بين أن τ₁ = R₁C متجانس مع الزمن.

3 ـ أ ـ بين أن:

$$\ln u_{R_1} = -\frac{t}{\tau_1} + \ln E$$

   ب ـ مثلنا البيان:

$$\ln u_{R_1} = f(t)$$

الشكل (2): ـ جد قيمة كل من $E$ و $\tau_1$.

ب ـ مثلنا البيان:  الشكل (2): ـ جد قيمة كل من E و τ₁

   ث ـ استنتج سعة المكلفة C

IIـ عند شحن المكثفة كليا وفي لحظة t = 0 نضع البادلة k في الوضع (2).

1 ـ بين أن المعادلة التفاضلية لتطور شحنة المكلفة تكتب على الشكل:

$\frac{dq}{dt} + \alpha q = 0$

حيث α ثابت يطلب تعيين عبارته بدلالة مميزات الدارة.

2 ـ تحقق أن العبارة q(t) = Q₀e^-αt و حلا للمعادلة التفاضلية.

حيث Q₀ الشحنة الأعظمية المخزنة في المكثفة.

3 ـ الشكل (3) يوضح المنحنى البياني q = f(t) لتطور شحنة المكثفة q خلال الزمن t

ـ جد قيمة كل من Q₀ وثابت الزمن τ₂ ، ثم استنتج قيمة المقاومة R₂.

4 ـ أ ـ اكتب العبارة الزمنية للطاقة المخزنة في المكثفة E_(c)(t).

   ب ـ احسب قيمتها عند اللحظتين: t₁ = 0s، t₂ = 0,6 s.

تصحيح الاختبار الثاني في مادة الفيزياء للسنة الثالثة ثانوي 2025/2024

حل التمرين الأول:(07 نقاط)

I ـ أ ـ قيمة الكتلة $m$: لدينا: $n = \frac{m}{M}$ و $n = C_0 V$ ومنه: $m = C_0 V M$
تطبيق عددي: $m = 0.1 \times 100 \times 10^{-3} \times 60$ ومنه: $m = 0.6 \, g$

   ب ـ البروتوكول التجريبي لتحضير المحلول (S₀):

بواسطة ميزان الكتروني حساس مضبوط نزن الكتلة m = 0,6 g من مسحوق حمض الايثانويك.

ـ نضيف الكتلة m = 6 g بالاعتماد على قمع في حوجلة عيارية سعتها 100 mL فيها  30 mLمن الماء المقطر مع الرج.

ـ نكمل بالماء المقطر حتى نصل لخط العيار مع الرج المستمر.

ـ على ملصقة نكتب اسم المحلول (S₀) وتركيزه المولي C₀ = 0,l mol/L.

2 ـ أ ـ معادلة التفاعل المنمذج للتحول الكيميائي بين حمض الايثانويك والماء:

CH₃COOH_(aq) + H₂O_(ℓ) = CH₃COO^-_(aq) + H₃O⁺_(aq)

   ب ـ التفاعل السابق تم بين حمض الثنائية CH₃COOH_(aq)/CH₃COO^-_(aq))) وأساس الثنائية الأخرى: (H₃O⁺_(aq)/H₂O_(ℓ))

3 ـ أ ـ جدول تقدم التفاعل:

CH3COOH(l) + H2O(ℓ) = H3O+(aq) + CH3COO-(aq)				معادلة التفاعل
كميات المادة n(mol)				التقدم	حالة الجملة
0	0	بزيادة	na	0	الحالة الابتدائية
x	x	بزيادة	na-x	x	الحالة الانتقالية
xf	xf	بزيادة	na -xf	xf	الحالة النهائية

   ب ـ حساب قيمة نسبة التقدم النهائي للتفاعل τ_f:

لدينا:

$$\tau_f = \frac{x_f}{x_{\text{max}}}$$

حيث: $x_f = [H_3O^+]_f V$ و $x_{\text{max}} = C_0 V$. وبالتالي:

$$\tau_f = \frac{[H_3O^+]_f V}{C_0 V} = \frac{[H_3O^+]_f}{C_0}$$

ومنه:

$$\tau_f = \frac{10^{-pH}}{C_0}$$

ومنه:

$$\tau_f = \frac{10^{-2.9}}{0.1}$$

ومنه:

$$\tau_f = 1.3\%$$

نستنتج أن حمض الإيثانويك ضعيف وأن التحول الكيميائي محدود (غير تام) لأن:

$$\tau_f < 100\% \quad \text{أو} \quad \tau_f < 1$$

   جـ ـ حساب قيمة ثابت التوازن $K$ للتفاعل:
لدينا: $K = \frac{[H_3O^+]_f [CH_3COO^-]_f}{[CH_3COOH]_f}$
ولدينا من جدول تقدم التفاعل: $[CH_3COO^-]_f = [H_3O^+]_f = \frac{x_f}{V}$
و: $[CH_3COOH]_f = \frac{C_0 V - x_f}{V} = C_0 - [H_3O^+]_f$
ومنه: $K = \frac{[H_3O^+]_f^2}{C_0 - [H_3O^+]_f}$ ومنه: $K = \frac{10^{-2pH}}{C_0 - 10^{-pH}}$
تطبيق عددي: $K = \frac{10^{-2(2.9)}}{0.1 - 10^{-2.9}} = 1.6 \times 10^{-5}$

II ـ 1 ـ أ ـ عبارة التركيز المولي 

$C$ للمحاليل $(Si)$ بدلالة $C_0$ و $V_0$ و $V_{H_2O}$:

لدينا حسب قانون التمديد:

$$C_0 V_0 = C_i V_i$$

ومنه:

$$C_i = C = \frac{C_0 V_0}{V_0 + V_{H_2O}}$$

حيث:

$$V_i = V_0 + V_{H_2O}$$

   ب ـ إتمام الجدول:

بالاعتماد على العلاقة:

$$C = \frac{C_0 V_0}{V_0 + V_{H_2O}} = \frac{0.1 \times 10}{10 + V_{H_2O}}$$

نملأ السطر الرابع.

ـ ندخل –log على طرفي المساواة و نملأ السطر الخامس.

المحاليل (Si)	(S1)	(S2)	(S3)	(S4)	(S5)	(S6)
V(H2O)(mL)	0	10	20	40	60	90
pH	2,9	3,05	3,15	3,25	3,30	3,40
C(mol/L)	0,10	0,05	0,033	0,02	0,014	0,01
- log(C)	1	1,3	1,48	1,7	1,85	2

   جـ ـ الخطوات العملية لتحضير المحلول (S₃):

ـ بواسطة ماصة عيارية سعتها 10 mL مزودة بإجاصة مص نأخذ حجما V₀ = 10 mL من المحلول (S₀).

ـ نسكبه في حوجلة عيارية سعتها 30 mL ثم نكمل بالماء المقطر حتى نصل لخط العيار مع الرج.

ـ على ملصقة نكتب اسم المحلول (S₃) و تركيزه المولي.

2 ـ أ ـ رسم البيان pH = f(-log(C)):

سلم الرسم: { pH: 1 cm → 0.5 -log(C): 1 cm → 0.2 }

   ب ـ المعادلة الرياضية للبيان:

البيان عبارة عن خط مستقيم مائل لا يمر من المبدأ، معادلته من الشكل: pH = A(-log(C)) + B

حيث:
A معامل توجيه البيان:

$$A = \frac{\Delta pH}{\Delta (-\log(C))} = \frac{3.4 - 2.9}{2 - 1} = 0.5$$

و B نقطة تقاطع البيان مع محور التراتيب:

$$B = 2.4$$

ومنه:

$$pH = 0.5 (-\log(C)) + 2.4$$

3 ـ أ ـ العلاقة النظرية بين pH و pK_a للثنائية CH₃COOH_(aq)/CH₃COO^-_(aq))):

لدينا:

$$\text{p}K_a = -\log K_a$$

ومنه:

$$\text{p}K_a = -\log \frac{[H_3O^+]_f [CH_3COO^-]_f}{[CH_3COOH]_f}$$

وبالتالي:

$$\text{p}K_a = \text{pH} - \log \frac{[CH_3COO^-]_f}{[CH_3COOH]_f}$$

ومنه:

$$\text{pH} = \text{p}K_a + \log \frac{[CH_3COO^-]_f}{[CH_3COOH]_f}$$

  ب ـ الإثبات بأن 

$\text{p}K_a = 2\text{pH} + \log C$

لدينا:

$$\text{pH} = \text{p}K_a + \log \frac{[CH_3COO^-]_f}{[CH_3COOH]_f}$$

وباستخدام العلاقة:

$$\frac{[CH_3COO^-]_f}{[CH_3COOH]_f} = \frac{[CH_3COO^-]_f}{C - [CH_3COO^-]_f}$$

وبإهمال $[CH_3COO^-]_f$ مقارنة بـ $C$:

$$\frac{[CH_3COO^-]_f}{[CH_3COOH]_f} \approx \frac{[CH_3COO^-]_f}{C}$$

نجد:

$$\text{pH} = \text{p}K_a + \log \frac{[CH_3COO^-]_f}{C}$$

وبتفكيك اللوغاريتم:

$$\text{pH} = \text{p}K_a + \log [CH_3COO^-]_f - \log C$$

أي:

$$\text{p}K_a = \text{pH} - \log [CH_3COO^-]_f + \log C$$

ونعلم أن:

$$[CH_3COO^-]_f = [H_3O^+]_f$$

وبالتعويض:

$$\text{p}K_a = \text{pH} - \log [H_3O^+]_f + \log C$$

وبما أن:

$$\text{pH} = -\log [H_3O^+]_f$$

نحصل على:

$$\text{p}K_a = 2\text{pH} + \log C$$

4 ـ استنتاج قيمة $pK_a$ للثنائية $\text{CH}_3\text{COOH} (aq)/\text{CH}_3\text{COO}^-(aq)$:

لدينا:

$$pK_a = 2pH + \log(C)$$

ومنه:

$$pH = \frac{1}{2} pK_a - \frac{1}{2} \log(C)$$

ومنه:

$$pH = \frac{1}{2} (-\log(C)) + \frac{1}{2} pK_a \quad \text{(1)}$$

بالمطابقة بين العلاقتين (1) و (2) طرف لطرف نجد:

$$\frac{1}{2} pK_a = 2.4$$

ومنه:

$$pK_a = 4.8$$

حل التمرين الثاني:(04,25 نقاط)

1 ـ الصفات التي تميز تفكك نواة مشعة معينة هي تلقاني، عشوائي، حتمي.

2 ـ تعريف النظائر: هي نكليدات لنفس العنصر الكيميائي لها نفس عدد البروتونات Z و تختلف في العدد الكتلي A أي تختلف في عدد النيترونات N.

3 ـ تركيب نواة الفوسفور : عدد البروتونات هو Z = 15 وعدد النيترونات هو N = A – Z = 32 – 15 = 17

4 ـ معادلة التفكك الموافقة لتحول نواة الفوسفور  وتحديد النواة الناتجة:

لدينا:

$${}_{15}^{32}P \rightarrow {}_{Z}^{A}X + {}_{-1}^{0}e^{-} + \bar{\nu}$$

حسب قانونا الانحفاظ لصودي نجد:

$$\begin{matrix} 32 = A + 0 \\ 15 = Z - 1 \end{matrix}$$

ومنه:

$$\begin{matrix} A = 32 \\ Z = 16 \end{matrix}$$

ومنه:

$$^{A}_{Z}X \equiv ^{32}_{16}S$$

ومنه:

$${}_{15}^{32}P\to {}_{16}^{32}S+{}_{-1}^0{e}^{-}+\bar{\nu }$$

والنواة الناتجة هي نواة الكبريت:

$$^{32}_{16}S$$

5 ـ تحديد زمن نصف العمر t_1/2 واستنتاج قيمة ثابت التفكك الإشعاعي λ:

لدينا:

$$A(t_{\frac{1}{2}}) = \frac{A_0}{2}$$

ومنه:

$$\frac{A(t_{\frac{1}{2}})}{A_0} = \frac{1}{2}$$

بالتالي نقرأ بيانياً:

$$t_{\frac{1}{2}} = 14 \, \text{j} = 1.2 \times 10^6 \, \text{s}$$

ومنه:

$$\lambda = \frac{\ln 2}{t_{\frac{1}{2}}} = 5.8 \times 10^{-7} \, \text{s}^{-1}$$

6 ـ أ ـ حساب عدد الأنوية الابتدائية للفوسفور 32:

$$N_0 = \frac{m_0}{M} N_A = 1.88 \times 10^{14} \, \text{noyaux}$$

   ب ـ استنتاج قيمة النشاط الإشعاعي A₀ للحقنة في اللحظة t₀ = 0:

$$A_0 = \lambda \cdot N_0 = 1.08 \times 10^8 \, \text{Bq}$$

7 ـ المدة الزمنية اللازمة لانعدام مفعول الدواء:

لدينا:

$$t = \frac{t_{\frac{1}{2}}}{\ln 2} \ln \left( \frac{A_0}{A(t)} \right)$$

ومنه:

$$t = \frac{14}{\ln 2} \ln \left( \frac{1.08 \times 10^8}{1.05 \times 10^6} \right) \approx 95 \, \text{j}$$

حل التمرين الثالث:(08,75 نقاط)

I ـ البادلة في اللحظة t = 0 عند الوضع (1):

1 ـ التمثيل على الدارة المدروسة جهة كل من التيار الكهربائي i و مثل أسهم التوترين u_C و u_R:

2 ـ أ ـ المعادلة التفاضلية لتطور شدة التيار i(t):

حسب قانون جمع التوترات نجد:

$$u_C + u_{R_1} = E$$

ومنه:

$$u_C + R_1 t = E$$

ومنه:

$$\frac{di}{dt} + \frac{1}{R_1 C} i(t) = 0$$

   ب ـ تحقق أن العبارة:

$$i(t) = \frac{E}{R_1} e^{\frac{-t}{\tau_1}}$$

حل للمعادلة التفاضلية:

لدينا:

$$\frac{di}{dt} = \frac{d}{dt} \left( \frac{E}{R_1} e^{\frac{-t}{R_1 C}} \right) = -\frac{1}{R_1 C} \left( \frac{E}{R_1} e^{\frac{-t}{R_1 C}} \right)$$

بالتعويض في المعادلة التفاضلية نجد:

$$-\frac{1}{R_1 C} \left( \frac{E}{R_1} e^{\frac{-t}{R_1 C}} \right) + \frac{1}{R_1 C} \left( \frac{E}{R_1} e^{\frac{-t}{R_1 C}} \right) = 0$$

ومنه:

$$0 = 0 \quad (\text{محققة})$$

ومنه:

$$i(t) = \frac{E}{R_1} e^{\frac{-t}{\tau_1}}$$

يمثل حل للمعادلة التفاضلية.

   ت ـ استنتاج عبارة التوتر $u_{R_1}(t)$ بين طرفي الناقل الأومي $R_1$:

من قانون أوم:

$$u_{R_1}(t) = R_1 \cdot i(t)$$

وبالتعويض عن $i(t)$:

$$u_{R_1}(t) = R_1 \cdot \frac{E}{R_1} e^{\frac{-t}{\tau_1}}$$

وبالتالي:

$$u_{R_1}(t)=E{e}^{\frac{-t}{{\tau }_1}}$$

   ث ـ التحليل البعدي للمقدار τ₁ = R₁C:

لدينا:

$$[R] \times [C] = \frac{[u]}{[i]} \times \frac{[i] \times [t]}{[u]} = [t] = T$$

ومنها: المقدار $R_1 C$ متجانس مع الزمن ووحدته الثانية $\, \text{s}$.

3 ـ أ ـ تبيان أن:

$$\ln(u_{R_1}) = -\frac{1}{\tau_1} t + \ln E$$

لدينا:

$$u_{R_1} = E e^{\frac{-t}{\tau_1}}$$

ومنه:

$$\ln(u_{R_1}) = -\frac{1}{\tau_1} t + \ln E \quad \text{→ (1)}$$

   ب ـ إيجاد قيمة كل من $E$ و $\tau_1$:

نلاحظ أن البيان $\ln(u_{R_1}) = f(t)$ عبارة عن خط مستقيم معادلته من الشكل:

$$\ln(u_{R_1}) = at + 1.8$$

ومنه:

$$\ln(u_{R_1}) = -10t + 1.8 \quad \text{→ (2)}$$

بالمطابقة بين العلاقتين (1) و (2) نجد:

$$\frac{1}{\tau_1} = 10 \quad \Rightarrow \quad \tau_1 = 0.1 \, \text{s}$$$$\ln E = 1.8 \quad \Rightarrow \quad E = 6 \, \text{V}$$

   ث ـ استنتاج سعة المكثف $C$:

لدينا:

$$\tau_1 = R_1 C$$

ومنه:

$$C = \frac{R_1}{R_1} = \frac{0.1}{10^3} = 10^{-4} \, \text{F}$$

II ـ 1 ـ تبيان أن المعادلة التفاضلية لتطور شحنة المكثف تكتب على الشكل: $\frac{dq}{dt} + \alpha q = 0$:

حسب قانون جمع التوترات:

$$u_{R_1} + u_{R_2} + u_C = 0$$

ومنه:

$$R_1 i + R_2 i + u_C = 0$$

لدينا:

$$u_C = \frac{q}{C}, \quad i = \frac{dq}{dt}$$

ومنه:

$$(R_1 + R_2) \frac{dq}{dt} + \frac{q}{C} = 0$$

ومنه:

$$\frac{dq}{dt} + \frac{1}{(R_1 + R_2)C} q(t) = 0$$

بالمطابقة نجد:

$$\alpha = \frac{1}{(R_1 + R_2)C}$$

2 ـ التحقق أن العبارة $q(t) = Q_0 e^{-\alpha t}$ حل للمعادلة التفاضلية:

لدينا:

$$q(t) = Q_0 e^{-\alpha t}$$

ومنه:

$$\frac{dq}{dt} = -Q_0 \alpha e^{-\alpha t}$$

بالتعويض في المعادلة التفاضلية نجد:

$$-Q_0 \alpha e^{-\alpha t} + \frac{Q_0 e^{-\alpha t}}{(R_1 + R_2)C} = 0$$

ومنه:

$$Q_0 e^{-\alpha t} \left( \alpha - \frac{1}{(R_1 + R_2)C} \right) = 0$$

ومنه:

$$\alpha = \frac{1}{(R_1 + R_2)}$$

3 ـ إيجاد قيمة كل من $Q_0$ وثابت الزمن $\tau_2$، ثم استنتاج قيمة المقاومة $R_2$:

بالاعتماد على البيان $q = f(t)$ نجد:

$$\tau_2 = 0.3 \, s$$

و

$$Q_0 = 0.6 \, mC$$

ولدينا:

$$\tau_2 = (R_1 + R_2) \times C$$

ومنه:

$$R_2 = \frac{\tau_2 - R_1 C}{C} = \frac{0.3 - 0.1}{10^{-4}} = 2 \, k\Omega$$

4 ـ أ ـ كتابة العبارة الزمنية للطاقة المخزنة في المكثف $E_C(t)$:

لدينا:

$$E_C(t) = \frac{1}{2} C u_C^2 (t) = \frac{1}{2} C \left( \frac{q(t)}{C} \right)^2$$

ومنه:

$$E_C(t) = \frac{1}{2} \frac{q(t)^2}{C} = \frac{1}{2} \frac{Q_0^2}{C} e^{\frac{-2t}{\tau_2}}$$

ومنه:

$$E_C(t) = \frac{1}{2} \frac{Q_0^2}{C} e^{\frac{-2t}{\tau_2}}$$

   ب ـ حساب قيمة الطاقة عند اللحظتين: $t_1 = 0 \, \text{s}$، $t_2 = 0.6 \, \text{s}$:

لدينا:

$$E_C(0) = 1.8 \times 10^{-3} \, \text{J}$$

ولدينا:

$$E_C(0.6) = 2.8 \times 10^{-5} \, \text{J}$$

الاختبار بصيغة الـ PDF

تصحيح الاختبار بصيغة الـ PDF