التطورات المهتزة. الاجابة عن أهم الأسئلة

في هذا الدرس، نستكشف عالم الاهتزازات من خلال تحليل التطورات المهتزة، سواء في الأنظمة الميكانيكية أو الكهربائية. سنتعرف على خصائص الحركة الاهتزازية، وأنواعها، وكيفية تمثيلها رياضيًا. كما سنقوم بالمقارنة بين الاهتزازات الميكانيكية مثل حركة النابض والنواس، والاهتزازات الكهربائية، الناتجة عن التفاعلات بين المكثفات والوشائع في الدارات الكهربائية.
هذا الدرس يُعتبر خطوة أساسية لفهم ظواهر موجية أكثر تعقيدًا، ويُستخدم في تطبيقات متعددة في الفيزياء، والهندسة والاتصالات.

ملاحظة: توجد وثيقة التلميذ بصيغة الـ PDF في نهاية المقال

I ـ الاهتزازات الحرة الميكانيكية:

1 ـ عرف الجملة الميكانيكية المهتزة؟

الجملة الميكانيكية المهتزة: هي كل جملة ميكانيكية، تقوم بحركة ذهاب واياب على جانبي وضع توازنها مثل: النواس المرن، الأرجوحة، النواس البسيط ...

2 ـ ذكر أنماط الاهتزازات:

تكون الاهتزازات الحرة على احدى الأنماط التالية:

* اهتزازات حرة غير متخامدة:

عندما تهتز الجملة، وتبقى طاقتها ثابتة خلال الزمن مثل: النواس البسيط المثالي.

فيديو يوضح الاهتزازات الحرة الغير متخامدة

*اهتزازات حرة متخامدة:

عندما تهتز الجملة، وتفقد جزء من طاقتها بفعل الاحتكاكات مثل: حركة النواس المرن.

فيديو يوضح اهتزازات حرة متخامدة

* اهتزازت حرة مغذاة:

عندما يتم تعويض كل الطاقة الضائعة باستمرار، ويتحقق ذلك بتجهيز مناسب مثل: رقاص ساعة حائطية.

3 ـ النواس المرن:

3 ـ 1 ـ عرف النواس المرن؟

هو جملة ميكانيكية تقوم بحركة ذهاب واياب على جانبي وضع توازنها.

3 ـ 2 ـ المعادلة التفاضلية باستخدام القانون الثاني لنيوتن، ومبدأ انحفاظ الطاقة (النواس المرن الأفقي):

حالة اهتزازات غير متخامدة:

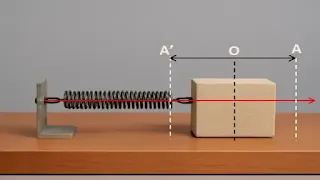
نحقق التركيب التالي، حيث نعتبر أن الاحتكاكات بين الجسم (S)، والمستوي الأفقي معدومة. 

نزيح الجسم (S) ذو الكتلة (m) عن وضع توازنه (O)، بسحبه أفقيا، ثم نتركه لحاله دون سرعة ابتدائية عند t = 0

ـ ماذا تلاحظ ؟

نلاحظ أن الجسم (S) يتحرك ذهابا وايابا، على جانبي (O) وضع التوازن، أي على طول القطعة [A’A]، وتتكرر الحركة بنفس الكيفية خلال فترات زمنية متساوية، ومتعاقبة، أي أن الحركة اهتزازية  دورية.

ـ هل الجملة (جسم + نابض) تتلقى طاقة من الوسط الخارجي؟

الجملة لا تتلقى طاقة من الوسط الخارجي. 

ـ ماذا نسمي هذا النوع من الاهتزازات ؟

نسمي هذا النوع من الاهتزازات (الاهتزازات الحرة).

ـ ماذا نسمي المقدار X₀ = A'A/2 ؟

نسمي المقدار X₀ = A'A/2 سعة الحركة.

ـ ما هو سبب الحركة الاهتزازية ؟

سبب الحركة، قوة يطبقها النابض (R) على الجسم (S)، تعمل على اعادته الى وضع توازنه (O)، وتتعلق بثابت المرونة، ومقدار الازاحة x، وتكون متجهة دوما نحو (O)

$$\vec{F}_{R/S} = -x \, \vec{i}$$

ـ ماذا نسمي الفترة الزمنية الفاصلة بين مرورين متتاليين للجسم (S) من نفس الموضع، وفي نفس الاتجاه ؟

نسمي الفترة الزمنية الفاصلة بين مرورين متتاليين للجسم (S) من نفس الموضع، وفي نفس الاتجاه الدور الذاتي للحركة، ونرمز له بالرمز T₀، ويعطى بالعبارة 

$$T_0=2\pi \sqrt{\frac{m}{K}}$$

ـ أثبت أن المقدار

$$\sqrt{\frac{m}{K}}$$

متجانس مع الزمن باستعمال التحليل البعدي؟

لدينا:

$$F = ma \Rightarrow [F] = \frac{[m][l]}{[t]^2}\Rightarrow [m] = \frac{[F][t]^2}{[l]}$$

ولدينا:

$$K = \frac{F}{x} \Rightarrow [K] = \frac{[F]}{[l]}$$

نحسب:

$$\frac{[m]}{[K]} = \frac{\frac{[F][t]^2}{[l]}}{\frac{[F]}{[l]}} = \frac{[F][t]^2}{[l]} \cdot \frac{[l]}{[F]} = [t]^2$$

ومنه:

$$\frac{[m]}{[K]}=[t{]}^2$$

ومنه:

$$\lfloor \sqrt{\frac{m}{k}} \rfloor = T$$

أثناء الدراسة التحريكية نهمل: كتلة النابض أمام m، كما نهمل كذلك الاحتكاكات الصلبة، ومقاومة الهواء. نعتبر الجسم (S) صلبا ونقطيا، نعتبر الجملة (S + نابض) جملة شبه معزولة، المعلم (OX) مرتبط بطاولة النضد الهوائي.

ـ بتطبيق القانون الثاني لنيوتن. أثبت أن:

$$\frac{d^{2}x}{d{t}^2}+\frac{K}{m}x(t)=0$$

بتطبيق القانون الثاني لنيوتن على الجسم (S) نجد:

$$\vec{P}+\vec{R}+\vec{F}=m\vec{a}$$

  بالإسقاط على المحور (OX) نجد: - F = m.a

ولدينا:

$$a=\frac{d^{2}x}{d{t}^2}$$

ومنه:

$$- Kx = m \frac{d^2 x}{dt^2}$$

ومنه:

$$\frac{d^{2}x}{d{t}^2}+\frac{K}{m}x=0$$

وهي معادلة تفاضلية من الرتبة الثانية.

ـ أثبت أن (x(t) = X₀cos(ω₀t +  φ ، يمثل حل للمعادلة التفاضلية السابقة ؟

حيث: 

 X₀ : سعة الحركة (m)

₀ω : نبض لحركة (s/rad)

φ : الصفحة الابتدائية (rad)

3 ـ 3 ـ استنتج عبارة الدور الذاتي للحركة ؟

معادلة الحركة الاهتزازية

$$\frac{d^2 x}{dt^2} + \frac{K}{m} x = 0$$

الحل المفترض

$$x(t) = X_0 \cos(\omega_0 t + \varphi)$$

حيث:

• $X_0$ هو سعة الاهتزاز.
• $\omega_0$ هو التردد الزاوي الطبيعي.
• $\varphi$ هو زاوية الطور.

حساب المشتقات

المشتقة الأولى:

$$\frac{dx}{dt} = -\omega_0 X_0 \sin(\omega_0 t + \varphi)$$

المشتقة الثانية:

$$\frac{d^2 x}{dt^2} = -\omega_0^2 X_0 \cos(\omega_0 t + \varphi)$$

وبما أن:

$$x(t) = X_0 \cos(\omega_0 t + \varphi)$$

فيمكننا كتابة المشتقة الثانية على النحو:

$$\frac{d^2 x}{dt^2} = -\omega_0^2 x(t)$$

بالمقارنة مع المعادلة التفاضلية

$$\frac{d^2 x}{dt^2} + \frac{K}{m} x = 0$$

نجد أن:

$$\omega_0^2 = \frac{K}{m}$$

وبأخذ الجذر التربيعي نجد:

$${\omega }_0=\sqrt{\frac{K}{m}}$$

ـ مثل بيان الدالة (x(t) = X₀cos(ω₀t + φ ؟

في حالة $\varphi = 0$

نجد:

$$x(t) = X_0 \cos(\omega_0 t)$$

ولدينا:

$$\omega_0 = \frac{2\pi}{T_0}$$

ومنه:

$$x(t)=X_0\cos \left(\frac{2\pi }{T_0}t\right)$$

من أجل قيم مختلفة للزمن نحصل على الجدول التالي:

T0	3T0/4	T0/2	T0/4	0	t(s)
X0	0	- X0	0	X0	x(m)

ـ استنتج عبارة الدور الذاتي للاهتزازات ؟

لدينا:

$$T_0 = \frac{2\pi}{\omega_0}$$

ولدينا:

$$\omega_0 = \sqrt{\frac{K}{m}}$$

ومنه:

$$T_0 = \frac{2\pi}{\sqrt{\frac{K}{m}}}$$

وباستخدام خاصية الجذور:

$$T_0=2\pi \sqrt{\frac{m}{K}}$$

ـ عرف التواتر، وأكتب عبارته ؟

التواتر هو عدد الاهتزازات، أو الدورات المنجزة خلال ثانية واحدة، ونرمز له بالرمز f₀ ، ويقاس بالهرتز، ويعطى بالعبارة التالية:

$$f_0 = \frac{1}{T_0} = \frac{\omega_0}{2\pi}$$

ـ أكتب عبارة السرعة، ومثلها بيانيا ؟

لدينا:

$$v(t)=\frac{dx}{dt}=-{\omega }_0{X}_0\sin ({\omega }_{0}t+\phi )$$

من أجل $\varphi = 0$، تصبح المعادلة:

$$v(t)=-{\omega }_0{X}_0\sin ({\omega }_{0}t)$$

نعلم أن:

$$\omega_0 = \frac{2\pi}{T_0}$$

ومنه:

$$v(t)=-{\omega }_0{X}_0\sin \left(\frac{2\pi }{T_0}t\right)$$

من أجل قيم مختلفة للزمن نحصل على الجدول التالي:

T0	3T0/4	T0/2	T0/4	0	t(s)
0	ω0.X0	0	ω0.X0 -	0	v(m)

ـ أكتب عبارة التسارع، ومثله بيانيا ؟

لدينا:

$$a(t)=\frac{d^{2}x}{d{t}^2}=-{\omega }_0^2{X}_0\cos ({\omega }_{0}t+\phi )$$

من أجل $\varphi = 0$، تصبح المعادلة:

$$a(t) = - \omega_0^2 X_0 \cos(\omega_0 t)$$

ولدينا:

$$\omega_0 = \frac{2\pi}{T_0}$$

ومنه:

$$a(t)=-{\omega }_0^2{X}_0\cos \left(\frac{2\pi }{T_0}t\right)$$

من أجل قيم مختلفة للزمن نحصل على الجدول التالي:

T0	3T0/4	T0/2	T0/4	0	t(s)
ω02.X0 -	0	ω02.X0	0	ω02.X0 -	a(m.s-2)

ـ أكتب عبارة طاقة الجملة (جسم + نابض) ؟

تملك الجملة (جسم + نابض) في أي لحظة طاقة حركية E_c = ½ m.v² ، وطاقة كامنة مرونية  E_pe= ½kx² 

حيث: E(t) = E_C(t) + E_pe(t) = cte

إذن طاقة الجملة شبه المعزولة (مثالية) محفوظة، أي قيمتها مقدار ثابت لا يتعلق بالزمن.

ـ أوجد المعادلة التفاضلية بتطبيق مبدأ انحفاظ الطاقة ؟

لدينا: E(t) = cte

ومنه: E(t) = ½ m v² + ½  kx² = cte

باشتقاق معادلة E(t) نجد: 

$$\frac{dE}{dt}=mv\frac{dv}{dt}+kx\frac{dx}{dt}=0$$

ومنه:

$$\frac{d^{2}x}{d{t}^2}+\frac{k}{m}x=0$$

وهي معادلة تفاضلية من الرتبة الثانية حلها جيبي من الشكل:

 (x(t) = X₀cos(ω₀t + φ  

ـ أرسم مخططات الطاقة بدلالة كل من t ، x ؟

رسم بيان  E = f(i) 

رسم بيان E = f(x)  

4 ـ النواس الثقلي:

ـ عرف النواس الثقلي؟

هو كل جسم صلب بإمكانه الاهتزاز حول محور ثابت أفقي، لا يمر من مركز عطالته مثل: الأرجوحة - رقاص الساعة الحائطية.  

ـ متى يكون النواس الثقلي في حالة توازن ؟

يكون النواس الثقلي في حالة توازن، عندما يكون مركز عطالته واقعا على نفس الشاقول مع نقطة تعليقه.

ـ أذكر حالات التوازن الممكنة ؟

أ ـ التوازن المستقر: 

يكون مركز عطالة النواس واقعا على نفس الشاقول مع نقطة تعليقه، وأسفل منها.

ب ـ التوازن القلق: 

يكون مركز عطالة النواس واقعا على نفس الشاقول مع نقطة تعليقه، وأعلى منها، ويسمى كذلك توازن مضطرب، أو غير مستقر.

ـ كيف تكون حالة حركة النواس الثقلي في حالة عدم وجود قوى احتكاك، وفي حالة وجودها ؟

أ ـ  حالة الحركة  دون احتكاكات: تكون الاهتزازات دورية غير متخامدة.

ب - حالة الحركة بالاحتكاك: نميز حالتين:

 * احتكاكات مائعة: 

تكون الحركة متخامدة بنظام شبه دوري أسي. 

* احتكاكات صلبة: 

تكون الاهتزازات متخامدة بنظام شبه دوري خطي.

يعتبر النواس البسيط حالة خاصة من النواس الثقلي ـ صف النواس البسيط ؟

يتألف من جسم نقطي كتلته m معلق إلى نقطة ثابتة بواسطة خيط خفيف، وعديم الامتطاط طوله ℓ

دراسة الحركة في حالة الاهتزازات الحرة غير المتخامدة:

نزيح كرة النواس بزاوية إزاحة ابتدائية θ₀ في اتجاه نعتبره الاتجاه الموجب، ونتركها دون سرعة ابتدائية، نلاحظ أن الكتلة تحاول الرجوع إلى الوضع الشاقولي بفعل قوة جذب الأرض.

ـ متى يكون النواس البسيط في حالة توازن ؟

يكون النواس في حالة توازن عندما يكون شاقوليا، ومركز عطالته واقعا أسفل  نقطة تعليقه.  

ـ كيف تكون حركة النواس؟

تكون حركة النواس دورية.

ـ ماهي العوامل المؤثرة في دور النواس البسيط ؟

أ ـ  يزداد دوره ببعد مركز عطالته عن محور الدوران (طول النواس ℓ).

ب ـ يزداد دوره بزيادة الارتفاع عن الأرض (نقصان الجاذبية g).

جـ ـ لا يتأثر دوره بالكتلة المعلقة.

ـ ماهي عبارة الدور الذاتي للنواس البسيط ؟

من أجل الاهتزازات صغيرة السعة نجد:

$$T_0=2\pi \sqrt{\frac{l}{g}}$$

من أجل السعات الكبيرة يعطى الدور بالعبارة التالية:

$$T=T_0(1+\frac{{\theta }_0^2}{16})$$

حيث:

 θ₀: سعة الاهتزاز (rad).  

T₀ : الدور الذاتي في حالة الاهتزازات صغيرة السعة.

الدراسة الطاقوية للنواس: 

المعادلة التفاضلية (خاص بشعبتي 3 ت ر ، 3 ر)

ـ أكتب عبارة طاقة الجملة (كتلة + أرض) ؟

إن الجملة (كتلة + أرض) تملك طاقة حركية، وطاقة كامنة ثقالية.  

E(t) = E_C + E_PP = cte

ـ أوجد المعادلة التفاضلية بتطبيق مبدأ انحفاظ الطاقة ؟

نعتبر المستوى المرجعي لقياس الطاقة الكامنة الثقالية، المستوي الأفقي المار بوضع التوازن.

من معادلة انحفاظ الطاقة نجد:

$$E_{C_1} + E_{PP_1} = E_{C_2} + E_{PP_2}$$

حيث:

$$E_{C_1} = 0$$

وبالتالي:

$$\frac{1}{2} m v^2 = m g h_1 - m g h_2$$

بما أن:

$$h_1 = l - l \cos\theta_0, \quad h_2 = l - l \cos\theta$$

فنحصل على:

$$\frac{1}{2} m v^2 = mg l (\cos\theta - \cos\theta_0)$$

ومنه:

$$v^2 = 2 g l (\cos\theta - \cos\theta_0)$$

باشتقاق المعادلة بالنسبة للزمن نجد:

$$2 v \frac{dv}{dt} = -2 g l \frac{d\theta}{dt} \sin\theta$$

وبما أن:

$$v = l \frac{d\theta}{dt}$$

فإننا نحصل على:

$$\frac{d^2 \theta}{dt^2} = -\frac{g}{l} \sin\theta$$

وبالنسبة للزوايا الصغيرة حيث $\sin\theta \approx \theta$ (بالراديان)، تصبح المعادلة:

$$\frac{d^2\theta }{d{t}^2}+\frac{g}{l}\theta =0$$

وهي معادلة تفاضلية من الرتبة الثانية.

ـ أثبت أن 

 θ(t) = θ₀cos(ω₀t + φ)  

يمثل حل للمعادلة التفاضلية السابقة ؟

حيث: 

 θ₀: سعة الحركة (rad)  

₀ω: نبض لحركة (s/rad)  

φ: الصفحة الابتدائية (rad)

ـ استنتج عبارة النبض الذاتي للحركة ؟

لدينا:

$$\frac{d^2 \theta}{dt^2} + \frac{g}{l} \theta = 0$$

الحل المقترح

$$\theta(t) = \theta_0 \cos(\omega_0 t + \varphi)$$

حساب المشتقات

• المشتقة الأولى:

$$\frac{d\theta}{dt} = - \omega_0 \theta_0 \sin(\omega_0 t + \varphi)$$

• المشتقة الثانية:

$$\frac{d^2 \theta}{dt^2} = - \omega_0^2 \theta_0 \cos(\omega_0 t + \varphi)$$

وبالتعويض عن $\theta(t)$:

$$\frac{d^2\theta }{d{t}^2}=-{\omega }_0^2\theta (t)$$

ومنه:

$$\frac{d^2 \theta}{dt^2} + \omega_0^2 \theta = 0$$

بالمقارنة بين المعادلتين التفاضليتين نجد:

$$\omega_0^2 = \frac{g}{l}$$

ومنه:

$${\omega }_0=\sqrt{\frac{g}{l}}$$

ولدينا:

$$T_0 = \frac{2\pi}{\omega_0}$$

ومنه:

$$T_0=2\pi \sqrt{\frac{l}{g}}$$

مفهوما الدور وشبه الدور:

أ ـ اذا كانت الاهتزازات حرة غير متخامدة، نسمي الفترة الزمنية الفاصلة بين مرورين متتاليين للجسم (S) من نفس الموضع وفي نفس الاتجاه، الدور الذاتي للحركة، ونرمز له بالرمز T₀ كما يوضحه التمثيل التالي:

ب ـ اذا كانت الاهتزازات حرة متخامدة، نسمي الفترة الزمنية الفاصلة بين مرورين متتاليين للجسم (S) من نفس الموضع وفي نفس الاتجاه، شبه الدور للحركة، ونرمز له بالرمز T كما يوضحه التمثيل التالي:

6 ـ تغذية الاهتزازات بتعويض التخامد:

المعادلة التفاضلية للاهتزازت المغذاة:

لا تخلو حركة أي مهتز ميكانيكي حقيقي من تخامد يؤدي الى تناقص سعته، وللحفاظ على سعة ثابتة يجب تعويض، وباستمرار الطاقة الضائعة بفعل الاحتكاك. يتم ذلك بواسطة أجهزة خاصة، مثل اضافة ثقل موازن لساعة حائطية، أو نابض حلزوني، كما في ساعة اليد.

ان تغذية الاهتزازات الميكانيكية تتم بتطبيق قوة اضافية على الجسم المهتز، لا تؤثر على السعة، بل بإمكانها أن تعوض بشكل مستمر كل الطاقة الضائعة، وتصبح السعة ثابتة.

ففي النواس الأفقي تصبح المعادلة التفاضلية من الشكل:

$$\frac{d^{2}x}{d{t}^2}+\frac{K}{m}x=0$$

وحلها من الشكل: (x(t) = X₀cos(ω₀t + φ

عبارة دور الاهتزاز المغذى:

أ ـ في حالة النواس المرن، يكون دور الاهتزازات المغذاة مساويا للدور الذاتي لاهتزازاته أي أن:

$$T=T_0=2\pi \sqrt{\frac{m}{K}}$$

ب ـ في حالة النواس البسيط، يكون دور الاهتزازات المغذاة مساويا للدور الذاتي لاهتزازاته أي أن:

$$T=T_0=2\pi \sqrt{\frac{l}{g}}$$

II ـ الاهتزازات الحرة لجملة كهربائية:

1 ـ تفريغ مكثفة في وشيعة (الدارة R,L,C):

المعادلة التفاضلية:

ـ ماهي الجملة الكهربائية المهتزة ؟

ندعو جملة كهربائية مهتزة، كل دارة تحتوي على وشيعة، مكثفة مشحونة، ومقاومة.

ـ متى تكون الاهتزازات الكهربائية متخامدة ؟

تكون الاهتزازات الكهربائية متخامدة، اذا كانت الدارة الكهربائية تحتوي على مقاومة، مع الوشيعة والمكثفة.

* نحقق دارة كهربائية كما بالشكل المقابل:

نعتبر مقاومة الدارة R = R₁+r

بواسطة الدارة 1 نحقق شحن المكثفة، وعند تمام الشحن نحول البادلة إلى الوضع 2

نوصل راسم اهتزاز بين طرفي المكثفة.

ـ ماذا تلاحظ ؟

نلاحظ المنحنى الموضح  بالشكل التالي:

ـ على ماذا يدل؟

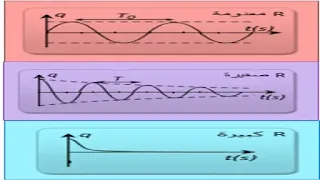
إن البيان يدل على أن التوتر بين طرفي المكثفة متخامد، ويلاحظ إزدياد هذا التخامد بزيادة المقاومة R الشكل (E)

ـ عند جعل مقاومة الدارة معدومة، على ماذا نحصل ؟

عند جعل مقاومة الدارة معدومة نحصل على منحنى الشكل (F) 

ـ كيف تكون الاهتزازات في هذه الحالة ؟

تكون الاهتزازات في هذه الحالة دورية غير متخامدة.

ـ باستخدام قانون التوترات. أوجد المعادلة التفاضلية للدارة RLC ؟

لدينا:

$$u_C + u_L + u_R = 0$$

حيث:

• $u_C$ هو التوتر بين طرفي المكثف.
• $u_L$ هو التوتر بين طرفي الوشيعة الصافية، ويمثل بـ $u_L = L \frac{di}{dt}$.
• $u_R$ هو التوتر بين طرفي المقاومة.

كما:

• $i = \frac{dq}{dt}$، حيث $i$ هو التيار، و $q$ الشحنة.
• $q = C u_C$، حيث $C$ هو السعة.

من خلال هذه المعادلات، نجد:

$$\frac{d^2{u}_C}{d{t}^2}+\frac{R}{L}\frac{d{u}_C}{dt}+\frac{1}{LC}{u}_C=0$$

وهي معادلة تفاضلية من الرتبة الثانية حلها خارج البرنامج.

- من أجل R صغيرة يكون النظام الكهربائي متخامد شبه دوري دورهT » T₀

- من أجل R كبيرة يكون  النظام الكهربائي لا دوري حرج.

- من أجل R = 0 (دارة مثاليةLC) تصبح المعادلة التفاضلية

$$\frac{d^2{u}_C}{d{t}^2}+\frac{1}{LC}{u}_C=0$$

 حلها جيبي (u_C(t) = Ecos(ω₀t + φ

نبضها الذاتي 

$${\omega }_0=\frac{1}{\sqrt{LC}}$$

دورها الذاتي 

$$T_0=2\pi \sqrt{LC}$$

نقول عن النظام الكهربائي في هذه الحالة  أنه دوري غير متخامد.

ملاحظة: 

يمكن اجراء الدراسة التحليلية للدارة R.L.C باستعمال شدة التيار i ، أو كمية الكهرباء q

ـ أكتب عبارة طاقة الجملة RLC  ؟

إن طاقة الدارة في أي لحظة هي طاقة الوشيعة، والمكثفة E = E_(C) + E_(L)

ـ أوجد المعادلة التفاضلية بتطبيق مبدأ انحفاظ الطاقة ؟

لدينا:

$$E(t) = \frac{1}{2} \frac{q^2 (t)}{C} + \frac{1}{2} L i^2 (t)$$

باشتقاق المعادلة بالنسبة للزمن نحصل على:

$$\frac{dE}{dt} = \frac{1}{C} q \frac{dq}{dt} + L i \frac{di}{dt}$$

وباستخدام العلاقة $i = \frac{dq}{dt}$، يمكن إعادة كتابة المعادلة كالتالي:

$$\frac{dE}{dt} = \left( \frac{1}{C} q + L \frac{d^2 q}{dt^2} \right) \frac{dq}{dt}$$

ومن المعادلة التفاضلية للدائرة RLC:

$$L \frac{d^2 q}{dt^2} + R \frac{dq}{dt} + \frac{1}{C} q = 0$$

نجد أن:

$$\frac{1}{C} q + L \frac{d^2 q}{dt^2} = - R i$$

وبالتعويض في معادلة الطاقة نحصل على:

$$\frac{dE}{dt} = - R i^2$$

أي أن التغير في الطاقة غير معدوم، مما يدا على أنه يوجد ضياع في الطاقة (فعل جول)، وسبب هذا الضياع هو وجود المقاومة.

ومن أجل دارة لا تحتوي على مقاومة فإن dE/dt = 0

ومنه:

$$\left(\frac{1}{C} q + L \frac{d^2 q}{dt^2} \right) \frac{dq}{dt} = 0$$

ومنه:

$$\frac{d^{2}q}{d{t}^2}+\frac{1}{LC}q=0$$

ـ أرسم مخططات الطاقة للدارة LC بدلالة كل من i ، t ؟

رسم بيان الدالة E = f(i)

رسم بيان الدالة  E = f(t)

ـ أرسم مخططات الطاقة للدارة RLC بدلالة t ؟

2 ـ تغذية الاهتزازات بتعويض التخامد:

المعادلة التفاضلية لاهتزاز مغذى:

ـ ما هو العامل المسبب للتخامد في الدارة الكهربائية المهتزة ؟

إن المسؤول عن تخامد الاهتزازات هو المقاومة.

ـ كيف يمكن تغذية الاهتزازات في الجملة الكهربائية المتخامدة ؟

يمكن تغذية الدارة بتوصيلها بجهاز(مضخم تطبيقي A.O) يعوض الطاقة الضائعة بفعل المقاومة حيث يلعب هذا الجهاز دور مقاومة سالبة.

ـ أكتب عبارة قانون التوترات في هذه الحالة ؟

يكون قانون التوترات كالتالي:

$$u_C + L \frac{di}{dt} + r i = R_0 i$$

عند $R_0 = r$، تصبح المعادلة:

$$u_C + L \frac{di}{dt} = 0$$

وباستخدام العلاقة $i = \frac{du_C}{dt}$، نحصل على:

$$L \frac{d}{dt} \left( \frac{du_C}{dt} \right) + u_C = 0$$

أو بشكل أوضح:

$$\frac{d^2{u}_C}{d{t}^2}+\frac{1}{LC}{u}_C=0$$

فيتحول بذلك النظام من اهتزازي متخامد إلى نظام اهتزازي مغذى غير متخامد.

عبارة دور الهزاز المغذى:

أ ـ في حالة الجملة الكهربائية، يكون دور الاهتزازات المغذاة مساويا للدور الذاتي لاهتزازاتها أي أن:

$$T_0=2\pi \sqrt{LC}$$

وثيقة التلميذ بصيغة الـ PDF