الاختبار الثاني في مادة الفيزياء للسنة الثالثة ثانوي2023

ملاحظة: يوجد الموضوع بصيغة الـ PDF في نهاية المقال

التمرين الأول: (9 نقاط)

من أجل معرفة طبيعة ثنائيي قطب X وY، نقوم بدراسة نظرية، ثم دراسة تطبيقية (تجربة):

1 ـ نرسم دارة كهربائية تحتوي مكثفة نعتبرها غير مشحونة، سعتها C مربوطة على التسلسل مع كل من ناقل أومي مقاومته R، مولد قوته المحركة الكهربائية E وقاطعة، نعتبر القاطعة مغلقة (عملية شحن المكثفة).

أ ـ أرسم الدارة الكهربائية ؟

ب ـ أوجد المعادلة التفاضلية للدارة بدلالةu_C  ؟

ج ـ تحقق أن حلها هو: u_C = E(1 – e^-t/RC)

د ـ مثل كيفياً تغيرات u_C بدلالة الزمن؟

هـ ـ ما هي دلالة نقطة تقاطع المماس للبيان عند المبدأ مع المستقيم u_C = E ؟

2 ـ نرسم دارة كهربائية تحتوي وشيعة مقاومتها الداخلية r، وذاتيتها L، وناقل أومي مقاومته R' متغيرة، ومولد مثالي لتوتر مستمر، وقاطعة مغلقة.

أ ـ أرسم الدارة الكهربائية ؟

ب ـ أوجد المعادلة التفاضلية للدارة بدلالة شدة التيارi(t) ؟

ج ـ بين أن i(t) = I(1 – e^-t/τ) يمثل حل للمعادلة التفاضلية السابقة ؟

د ـ استنتج عبارة فرق الكمون بين طرفي الوشيعة ؟

هـ ـ أرسم كيفيا البيان الذي يمثل فرق الكمون بين طرفي الوشيعة:

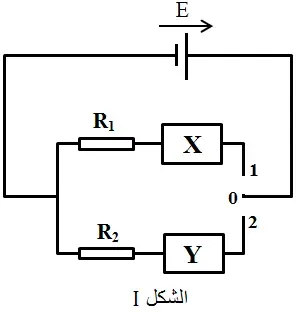
3 ـ نحقق التركيب التجريبي الموضح في الشكل ـ I، حيث: X وY ثنائيي قطب يمكن أن يكونا مكثفة سعتها C، مقاومة R، أو وشيعة ذاتيتها L ولها مقاومة داخلية r، R₁ = 100 Ω ، R₂ = 20 Ω

نستعمل جهاز EXAO متصل بجهاز الكمبيوتر، من أجل مراقبة التغير في التوتر بين طرفي كل من ثنائيي القطب X وY، عند غلق القاطعة في الوضع ـ 1، نلاحظ على شاشة جهاز الكمبيوتر البيان الموضح في الشكل ـ 1، وعند غلق القاطعة في الوضع ـ 2، نلاحظ على شاشة جهاز الكمبيوتر البيان الموضح في الشكل ـ 2، ونقرأ على لاقط شدة التيار الكهربائي، القيمة الأعظمية I = 0,5 A

بالاعتماد على البيانين:

أ ـ استنتج العنصرين X وY ؟

ب ـ استنتج قيمة ثابت الزمن في كل حالة ؟

ج ـ استنتج قيمة القوة المحركة الكهربائية للمولد ؟

د ـ استنتج سعة المكثفة C اذا كان أحد العنصرين X أوY يمثل مكثفة ؟

هـ ـ استنتج قيمتي L ، r اذا كان أحد العنصرين X  أوY يمثل مكثفة ؟

التمرين الثاني: (5.5 نقاط)

من أجل الدفاع عن النفس، النمل يستعمل تأشيراته (mandibules) وحمض النمل (حمض الميثانويك)، التأشيرات تستعمل لتثبيت العدو، بينما حمض النمل يستعمل لقتله: عندما تحس نملة بالخطورة تقف على رجليها الأخيرتين، ثم ترش العدو بحمض النمل على بعد 30 cm بواسطة جذعها (Abdomen)

نريد دراسة بعض خواص حمض النمل الذي ينحل في الماء، وصيغته HCOOH

1 ـ نضع في حوجلة عيارية سعتها V₁ = 100 ml كتلة m من حمض الميثانويك، ثم نكمل الحجم الى خط العيار بواسطة الماء المقطر. بعد الرج نحصل على محلول (S₁) لحمض الميثانويك تركيزه المولي C₁ = 10^-2 mol.L^-1.

أ ـ أحسب m ؟

ب ـ أكتب معادلة تفاعل حمض الميثانويك مع الماء ؟

ج ـ قدم جدولا لتقدم التفاعل ؟

د ـ عبر عن النسبة النهائية لتقدم التفاعل بدلالة [H₃O⁺]_f1 وC₁ ؟

هـ ـ اعط عبارة Q_rf1 لكسر النهائي للتفاعل وبين أن

$Q_{rf_1} = \frac{\left[\text{H}_3\text{O}^+\right]_{f_1}^2}{C_1 - \left[\text{H}_3\text{O}^+\right]_{f_1}}$

2 ـ أعط عبارة الناقلية النوعية σ للمحلول عند حالة التوازن بدلالة الناقلية النوعية المولية للشوارد المتواجدة فيه، و [H₃O⁺]_f

3 ـ إن قياس الناقلية النوعية للمحلول (S₁)، أعطى σ₁ = 0,051 S.m^-1 عند 25°C

   ـ عين Q_rf1، ثم قارن قيمته التجريبية مع ثابت الحموضة K_a للثنائية HCOOH/HCOO^- ؟

4 ـ نحقق نفس الدراسة السابقة، ولكن باستعمال محلول (S₂) لحمض النمل، تركيزه المولي C₂ = 0,10 mol.L^-1 لنحصل على النتائج التالية:

 Q_rf2 = 1,8.10^-4، σ₂ = 0,170 S.m^-1

أ ـ هل يؤثر التركيز المولي للمحلول على النسبة النهائية للتقدم τ_f ؟

ب ـ هل يؤثر التركيز المولي للمحلول على Q_rf عند حالة التوازن ؟

المعطيات:

M(C) = 12 g.mol^-1 ، M(H) = 1 g.mol^-1 ، M(O) = 16 g.mol^-1

ثابت الحموضة عند 25°C: K_a = 1,8.10^-4

الناقلية النوعية المولية للشوارد عند 25°C

λ(H₃O⁺) = 35.10^-3S.m².mol^-1

λ(HCOO^-) = 5,46.10^-3S.m².mol^-1

التمرين الثالث: (5.5 نقاط)

نعطي مخطط (Z – N) أو ما يسمى بمخطط سيقري.

1 ـ عرف النواة المشعة ؟

2 ـ بالاعتماد على المخطط اعط تركيب كل نواة ؟

3 ـ أكتب معادلات التفاعلات النووية (1)، (2)، (3) و(4) المشار اليها في المخطط ؟

4 ـ استنتج نوع النشاط الاشعاعي بالنسبة لكل تفاعل؟

5 ـ تعرف على النواتين: X وY ؟ 

6 ـ ماذا يمكن القول عن النواتين X وPb ؟

7 ـ اذا علمت أن زمن نصف العمر للبولونيوم 210 هو t_1/2 = 138 j، وأن نشاط عينة منه في اللحظة t = 0 هو A₀ = 10¹⁰ Bq، أحسب:

أ ـ ثابت النشاط الاشعاعي λ ؟

ب ـ عدد الأنوية الابتدائية N₀ للبولونيوم 210 ؟

ج ـ المدة الزمنية التي يصبح فيها عدد أنوية العينة، مساويا لسدس ما كان عليه في اللحظة t = 0 ؟

نعطي مستخرج من الجدول الدوري:

العنصر	ذهب	زئبق	ثالوم	رصاص	بزموث	بولونيوم	استات	رادون
الرمز	Au	Hg	Tl	Pb	Bi	Po	At	Rn
العدد الذري	79	80	81	82	83	84	85	86

تصحيح الاختبار الثاني في مادة العلوم الفيزيائية

تصحيح التمرين الأول: (9 نقاط)

1 ـ أ ـ رسم الدارة الكهربائية:

ب ـ ايجاد المعادلة التفاضلية للدارة بدلالةu_C :

لدينا: E – u_C – u_R = 0 

ومنه: E = u_C + u_R

وحسب قانون أوم: u_R = R.i 

ومنه: u_C + R.i = E

لدينا:

$$i=\frac{dq}{d\mathrm{t}}$$

باستخدام العلاقة $dq = C \cdot du_C$، تصبح:

$$i=C\cdot \frac{d{u}_C}{dt}$$

ومنه:

$$u_C+RC\cdot \frac{d{u}_C}{dt}-E=0$$

بقسمة طرفي المعادلة على $RC$ وترتيبها، نحصل على:

$$\frac{d{u}_C}{dt}+\frac{1}{RC}{u}_C(t)-\frac{E}{RC}=0$$

ج ـ التحقق من أن u_C(t) = E(1 – e^-t/RC) حل للمعادلة التفاضلية السابقة:

لدينا: u_C(t) = E(1 – e^-t/RC) 

ومنه: u_C(t) = E – Ee^-t/RC → (2)

ومنه: 

$$\frac{d{u}_C}{dt}=\frac{E}{RC}{e}^{\frac{-t}{RC}}\to (3)$$

بتعويض (2) و(3)، نحصل على:

$$\frac{E}{RC}{e}^{\frac{-t}{RC}}+\frac{1}{RC}(E-E{e}^{\frac{-t}{RC}})-\frac{E}{RC}=0$$

ومنه:

$$\frac{E}{RC}{e}^{\frac{-t}{RC}}+\frac{E}{RC}-\frac{E}{RC}{e}^{\frac{-t}{RC}}-\frac{E}{RC}=0$$

ومنه: 0 = 0 (محققة) 

ومنه:  u_C(t) = E(1 – e^-t/RC)حل للمعادلة التفاضلية (1)

د ـ تمثيل تغيرات u_C بدلالة الزمن كيفياً:

من أجل t = 0 نجد: u_C(0) = 0

ومن أجل t = τ نجد: u_C(τ) = 0,63E

ومن أجل t = 5τ نجد:  u_C(5τ) ≈ E

هـ ـ نقطة تقاطع المماس للبيان عند المبدأ مع المستقيم u_C = E هي النقطة التي فاصلتها تمثل ثابت الزمن τ.

2 ـ أ ـ رسم الدارة الكهربائية:

ب ـ ايجاد المعادلة التفاضلية للدارة بدلالة شدة التيار i(t):

لدينا: u_B + u_R = E → (1)

ولدينا: u_R = R.i → (2)

ولدينا:

$$u_B=L\frac{di}{dt}+r\cdot i\to (3)$$

بتعويض (2) و(3)، نجد:

$$L\frac{di}{dt}+r\cdot i+R\cdot i=E$$

ومنه:

$$L\frac{di}{dt}+r\cdot i+R\cdot i-E=0$$

بإعادة الترتيب:

$$L\frac{di}{dt}+(r+R)\cdot i-E=0$$

وبقسمة طرفي المعادلة على $L$ نجد:

$$\frac{di}{dt}+\frac{(r+R)}{L}i(t)-\frac{E}{L}=0$$

ولدينا:

$$\frac{(r+R)}{L}=\frac{1}{\tau },\text{و}E=(R+r)I$$

ومنه:

$$\frac{di}{dt}+\frac{1}{\tau }i(t)-\frac{I}{\tau }=0\to (4)$$

ج ـ الاثبات بأن i(t) = I(1 – e^-t/τ) يمثل حل للمعادلة التفاضلية السابقة:

لدينا: i(t) = I(1 – e^-t/τ)

ومنه: i(t) = I – Ie^-t/τ → (1)

ولدينا:

$$\frac{di}{dt} = I \frac{(R + r)}{L} e^{\frac{-t}{\tau}} \quad \rightarrow \quad (2)$$

بتعويض (1) و(2) في (4)، و التبسيط نجد:

$$\frac{(r+R)}{L}I-\frac{E}{L}=0$$

ولدينا:

$$(r+R)I=E$$

ومنه:

$$\frac{E}{L}-\frac{E}{L}=0$$

ومنه: (0 = 0) محققة

ومنه:  i(t) = I(1 – e^-t/τ)يمثل حل للمعادلة التفاضلية (4)

د ـ استنتاج عبارة فرق الكمون بين طرفي الوشيعة:

لدينا:

$$u_B=L\frac{di}{dt}+r\cdot i\to (\ast )$$

لدينا: i(t) = I(1 – e^-t/τ)

ومنه: i(t) = I – Ie^-t/τ → (1)

ولدينا:

$$\frac{di}{dt}=I\frac{(R+r)}{L}{e}^{\frac{-t}{\tau }}\to (2)$$

بتعويض (1) و(2) في (*)، نجد:

$$u_B=LI\frac{(R+r)}{L}{e}^{\frac{-t}{\tau }}+r(I-I{e}^{\frac{-t}{\tau }})$$

ومنه:

$$u_B=LI\frac{(R+r)}{L}{e}^{\frac{-t}{\tau }}+rI-rI{e}^{\frac{-t}{\mathrm{\tau }}}$$

ومنه: u_B = I(R + r)e^-t/τ + rI – rIe^-t/τ

ومنه:  u_B = RIe^-t/τ + rI

حيث:

$$I=\frac{E}{R+r}$$

هـ ـ رسم البيان الذي يمثل فرق الكمون بين طرفي الوشيعة:

لدينا: u_B = RIe^-t/τ + rI 

حيث:

$$I = \frac{E}{R + r}, \quad \tau = \frac{L}{R + r}$$

من أجل t = 0 نجد: u_B(0) = E

ومن أجل t = τ نجد:

u_B(τ) = 0,37RI + rI

ومن أجل t = 5τ نجد:  u_B(5τ) ≈ rI

3 ـ أ ـ استنتاج العنصرين X وY:

من خلال الدراستين النظرية، والتجريبية، نستنتج أن العنصر X عبارة عن مكثفة سعتها C، أما العنصرY فهو عبارة عن وشيعة ذاتيتها L ولها مقاومة داخلية r

ب ـ استنتاج قيمة ثابت الزمن في كل حالة:

في حالة دارة المكثفة، من البيان(1) نجد: τ = 0,05 s

في حالة دارة الوشيعة، من البيان(2) نجد: τ' = 4.10^-3 s

ج ـ استنتاج قيمة القوة المحركة الكهربائية للمولد:

بالاعتماد على البيانين نجد: E = 12 V

د ـ استنتاج سعة المكثفة C:

لدينا:

$$\tau =R_1\cdot C$$

ومنه:

$$C=\frac{\tau }{R_{\mathrm{1}}}$$

وبتعويض القيم:

$$C=\frac{0.05}{\mathrm{100}}$$

ومنه: C = 5.10^-4 F

هـ ـ استنتاج قيمتي r ، L:

 من البيان (2) نجد أنه في النظام الدائم: u_B = r.I = 2

 ومنه:

$$r = \frac{u_B}{I}$$

وبتعويض القيم:

$$r = \frac{2}{0.5}$$

ومنه:

$$r = 4$$

ولدينا:

$${\tau }^{\mathrm{\prime }}=\frac{L}{R_2+\mathrm{r}}$$

ومنه: L = τ'(R₂ + r) 

ومنه: L = 4.10^-3(20 + 4) 

ومنه: L = 9,6.10^-2H

تصحيح التمرين الثاني: (5.5 نقاط)

1 ـ أ ـ حساب m:

لدينا: m = C₁.M.V₁ 

حيث: M = 46 g/mol

ومنه: m = 10^-2.46.0,1 

ومنه: m = 4,6.10^-2 g

ب ـ كتابة معادلة تفاعل حمض الميثانويك مع الماء:

HCOOH_(aq) + H₂O_(l) = H₃O⁺_(aq) + HCOO^-_(aq)

ج ـ انجاز جدول تقدم التفاعل:

HCOOH(aq) + H2O(l) = H3O+(aq) + HCOO-(aq)				معادلة التفاعل
كميات المادة n(mol)				التقدم	حالة الجملة
0	0	بزيادة	n0	0	الحالة الابتدائية
x	x	بزيادة	n0-x	x	الحالة الانتقالية
xf	xf	بزيادة	n0 -xf	xf	الحالة النهائية

د ـ التعبير عن النسبة النهائية لتقدم التفاعل بدلالة [H₃O⁺]_f1 وC₁:

لدينا:

$$\tau_{f_1} = \frac{x_{f_1}}{x_{\text{max}_1}}$$

حيث:

$$x_{f_1}=[{\text{H}}_3{\text{O}}^{+}{]}_{f_1}\cdot V_1,x_{{\text{max}}_1}=C_1\cdot V_{\mathrm{1}}$$

ومنه:

$$\tau_{f_1} = \frac{[\text{H}_3\text{O}^+]_{f_1} \cdot V_1}{C_1 \cdot V_1}$$

ومنه:

$${\tau }_{f_1}=\frac{[{\text{H}}_3{\text{O}}^{+}{]}_{f_1}}{C_1}$$

هـ ـ إعطاء عبارة Q_rf1 لكسر النهائي للتفاعل والتبيين بأن

$$Q_{r{f}_1}=\frac{[H_3{O}^{+}{]}_{f_1}^2}{C_1-[H_3{O}^{+}{]}_{f_1}}$$

لدينا:

$$Q_{rf_1} = \frac{[\text{H}_3\text{O}^+]_{f_1} \cdot [\text{HCOO}^-]_{f_1}}{[\text{HCOOH}]_{f_1}}$$

حيث:

$$[\mathrm{H_3O^+}]_{f_1} = [\mathrm{HCOO^-}]_{f_1}$$

وكذلك:

$$[\mathrm{HCOOH}]_{f_1} = C_1 - [\mathrm{H_3O^+}]_{f_1}$$

ومنه:

$$Q_{r{f}_1}=\frac{[{\text{H}}_3{\text{O}}^{+}{]}_{f_1}^2}{C_1-[{\text{H}}_3{\text{O}}^{+}{]}_{f_1}}$$

2 ـ إعطاء عبارة الناقلية النوعية σ₁ للمحلول عند حالة التوازن بدلالة الناقلية النوعية المولية للشوارد المتواجدة فيه، و[H₃O⁺]_f1:

لدينا:

σ₁ = [H₃O⁺]_f1.λ(H₃O⁺) + [H₃O⁺]_f1.λ(HCOO^-)

ومنه:

σ₁ = [H₃O⁺]_f1(λ(H₃O⁺) + λ(HCOO^-))

3 ـ تعيين Q_rf1، ثم مقارنة قيمته التجريبية مع ثابت الحموضة K_a للثنائية HCOOH/HCOO^-

لدينا:

$$[\text{H}_3\text{O}^+]_{f_1} = \frac{\sigma_1}{\lambda_{\text{H}_3\text{O}^+} + \lambda_{\text{HCOO}^-}}$$

ومنه:

$$[\mathrm{H_3O^+}]_{f_1} = \frac{0{,}051}{(35 + 5{,}46) \times 10^{-3}}$$

ومنه:

$$[\mathrm{H_3O^+}]_{f_1} = 1{,}26 \ \mathrm{mol \cdot m^{-3}}$$

وبعد التحويل إلى $\text{mol} \cdot \text{L}^{-1}$:

$$[\text{H}_3\text{O}^+]_{f_1} = 1.26 \times 10^{-3} \, \text{mol} \cdot \text{L}^{-1}$$

ومنه:

$$Q_{rf_1} = \frac{(1.26 \times 10^{-3})^2}{(10^{-2}) - 1.26 \times 10^{-3}}$$

ومنه:

$$Q_{rf_1} = \frac{1.59 \times 10^{-6}}{0.87 \times 10^{-2}}$$

ومنه:

$$Q_{rf_1} = 1.8 \times 10^{-4}$$

وأخيرًا:

$$Q_{r{f}_1}=K_a$$

أ ـ دراسة مدى تأثير التركيز المولي للمحلول على النسبة النهائية للتقدم τ_f:

لدينا:

$$\tau_{f_1} = \frac{[\text{H}_3\text{O}^+]_{f_1}}{C_1}$$

و:

$$\tau_{f_2} = \frac{[\text{H}_3\text{O}^+]_{f_2}}{C_2}$$

حيث:

$$[\mathrm{H_3O^+}]_{f_2} = \frac{0{,}17}{35 + 5{,}46}$$

ومنه:

$$[\mathrm{H_3O^+}]_{f_2} = 4{,}20 \times 10^{-3} \ \mathrm{mol \cdot L^{-1}}$$

ومنه:

$$\tau_{f_1} = \frac{1.23 \times 10^{-3}}{10^{-2}} = 0.123$$

ومنه:

$${\tau }_{f_2}=\frac{4.20\times 10^{-3}}{0.10}=4.20\times 10^{-2}$$

نلاحظ أنه من أجل C₁ ≠ C₂ وجدنا أن τ_f1 ≠ τ_f2 ، ومنه نستنتج أن النسبة النهائية لتقدم التفاعل تتعلق بالحالة الابتدائية للجملة.

ب ـ دراسة مدى تأثير التركيز المولي للمحلول على Q_rf عند حالة التوازن:

لدينا:

$$Q_{rf_2} = \frac{(4.20 \times 10^{-3})^2}{0.10 - 4.20 \times 10^{-3}}$$

ومنه:

$$Q_{rf_2} = \frac{17.64 \times 10^{-6}}{0.96 \times 10^{-1}}$$

ومنه:

$$Q_{r{f}_2}=1.8\times 10^{-4}$$

نلاحظ أنه من أجل C₁ ≠ C₂ وجدنا أن Q_rf1 = Q_rf2 ، ومنه نستنتج أن كسر التفاعل النهائي لا يتعلق بالتراكيز الابتدائية للحمض في المحلول.

تصحيح التمرين الثالث: (5.5 نقاط)

1 ـ تعريف النواة المشعة: هي نواة غير مستقرة، لا تحافظ على تركيبها ويحدث لها تفكك

2 ـ اعطاء تركيب كل نواة:

النواة	العدد الذري Z	عدد النيترونات N	العدد الكتلي A
Po	84	131	215
X	82	129	211
Bi	83	128	211
Y	81	126	207
Pb	82	125	207

3 ـ كتابة معادلات التفاعلات النووية (1)، (2)، (3) و(4) المشار اليها في المخطط:

لدينا:

$${}_{84}^{215}\text{Po}{\to }_{82}^{211}X{+}_2^4\text{He}$$$${}_{82}^{211}X{\to }_{83}^{211}\text{Bi}{+}_{-1}^0{e}^{-}+\bar{V}$$$${}_{83}^{211}\text{Bi}{\to }_{81}^{207}\text{Y}{+}_2^4\text{He}$$$${}_{81}^{207}\text{Y}{\to }_{82}^{207}\text{Pb}{+}_{-1}^0{e}^{-}+\bar{V}$$

4 ـ استنتاج نوع النشاط الاشعاعي بالنسبة لكل تفاعل:

من خلال معادلات التفاعلات النووية نستنتج أن:

النشاط (1) من نوع α

النشاط (2) من نوع β^-

النشاط (3) من نوع α

النشاط (4) من نوع β^-

5 ـ التعرف على النواتين: X وY: 

بالاعتماد على التفاعلات النووية، والمستخرج من الجدول الدوري نستنتج أن النواة X هي نواة الرصاص 211 ، و النواة Y هي نواة الثاليوم 207.

6 ـ يمكن القول عن النواتين X وPb أنهما نظيران

7 ـ أ ـ حساب ثابت النشاط الاشعاعي λ:

لدينا:

$$\lambda = \frac{\ln 2}{t_{1/2}}$$

ومنه:

$$\lambda = \frac{0.69}{138} = 5 \times 10^{-3} \, \text{j}^{-1}$$

وأيضًا:

$$\lambda =\frac{0.69}{138\times 24\times 3600}=5.79\times 10^{-8}{\text{s}}^{-1}$$

ب ـ حساب عدد الأنوية الابتدائية N₀ للبولونيوم 210:

لدينا:

$$A_0 = \lambda N_0$$

ومنه:

$$N_0 = \frac{A_0}{\lambda}$$

وبتعويض القيم:

$$N_0=\frac{10^{10}}{5.79\times 10^{-8}}=1.73\times 10^{17}\text{noyaux}$$

ج ـ حساب المدة الزمنية التي يصبح فيها عدد أنوية العينة مساويا لسدس ما كان عليه في اللحظة t = 0:

لدينا:

$$N(t) = N_0 e^{-\lambda t}$$

ومنه:

$$\frac{N(t)}{N_0} = e^{-\lambda t} = \frac{1}{6}$$

وبالتالي:

$$-\lambda t = \ln 6$$

ومنه:

$$t = \frac{\ln 6}{\lambda} = \frac{1.79}{5.79 \times 10^{-8}} = 3.1 \times 10^7 \, \text{s}$$

ومنه:

$$t=357.8\text{j}$$

الموضوع بصيغة الـ PDF