الظواهر الكهربائية. دراسة ثنائي القطبRL 

الظواهر الكهربائية، تلعب دورًا محوريًا في فهم كيفية عمل الدارات الكهربائية. من بين هذه الدراسات، يُعد تحليل ثنائي القطب RL، أحد الموضوعات الأساسية في الإلكترونيات والكهرباء. دعونا نتعمق أكثر في الإجابة عن الأسئلة المرتبطة بهذا الموضوع، ثنائي القطب RL هو مكوّن كهربائي، يحتوي على مقاومة (R)، ووشيعة تحريضية (L). يتم استخدامه في تحليل التيارات والتوترات في الدارات الكهربائية، حيث تمثل المقاومة مقاومة مرور التيار، بينما يعبر التحريض عن القدرة على تخزين الطاقة على شكل مجال مغناطيسي.

ملاحظة: توجد وثيقة التلميذ بصيغة الـ PDF في نهاية المقال.

IV ـ دراسة ثنائي القطبRL :

1 ـ تعريف الوشيعة:

هي ثنائي قطب يتكون من سلك معدني طويل ومعزول، ملفوف حول أسطوانة عازلة، ويمكن أن تكون للوشيعة مقاومة داخلية نرمز لها بالرمز r، وتتميز كل وشيعة بمقدار فيزيائي خاص بها يسمى معامل التحريض الذاتي، أو ذاتية الوشيعة L، وتقاس بوحدة تسمى الهنري H، يوجد في بعض الوشائع نواة حديدية لزيادة نفاذيتها المغناطيسية، يرمز للوشيعة في الدارات الكهربائية بأحد الرمزين التاليين: 

2 ـ تطور شدة التيار الكهربائي المار في وشيعة تحريضية :

نشاط ـ 2 ـ

نحقق الدارة الكهربائية الموضحة بالشكل التالي:

نوصل راسم اهتزاز مهبطي مزود بذاكرة بين الوشيعة والناقل الأومي

(يستعمل راسم الاهتزاز المهبطي المزود بذاكرة، لتسجيل التوتر اللحظي في الظواهر الكهربائية السريعة، التي لا تستطيع العين المجردة مجاراتها).

ـ نميز حالتين: عند غلق القاطعة يظهر المنحنى 1، وعند فتح القاطعة يظهر المنحنى 2

ـ فسر كل حالة ؟

ـ يمثل المنحنى (1) تغير التوتر الكهربائي بين طرفي الوشيعة بدلالة الزمن في حالة دارة مغلقة، حيث أن البيان يتناقص وفق دالة أسـية دون أن يصل الى قيمة معدومة، وذلك لأن الوشيعة لها مقاومة داخلية

ـ يمثل المنحنى (2) تغير التوتر الكهربائي بين طرفي الوشيعة بدلالة الزمن في حالة دارة مفتوحة، حيث أن البيان يتزايد وفق دالة أسـية من قيمة أعظمية سالبة الى قيمة معدومة.

ـ استنتج عبارة التوتر بين طرفي الوشيعة ؟

حالة دارة مغلقة: u_B = ae^-bt + d

حالة دارة مفتوحة: u_B = - ae^-bt

3 ـ دراسة الدارةRL :  

3 ـ 1 ـ حالة غلق القاطعة :

 نحقق الدارة الكهربائية التالية:

بتطبيق قانون التوترات، وعبارة التوتر بين طرفي الوشيعة، وعبارة التوتر بين طرفي الناقل الأومي

ـ اثبت العلاقة التالية:

$$\frac{di}{dt} + \frac{(R+r)i}{L} - \frac{E}{L} = 0$$

الإثبات:

1. وفقاً لقانون جمع التوترات، لدينا:

   $$u_B + u_R = E \tag{1}$$

2. حسب العلاقة بين الجهد والمقاومة:

   $$u_R = R \cdot i \tag{2}$$

3. وللجهد عبر الوشيعة، فإن:

   $$u_B = L \frac{di}{dt} + r \cdot i \tag{3}$$

بالتعويض:

نعوّض العلاقات (2) و(3) في المعادلة (1):

بتبسيط الطرف الأيسر نجد:

$$L \frac{di}{dt} + (R + r) \cdot i - E = 0$$

إعادة الترتيب:

بقِسمة جميع الأطراف على $L$:

$$\frac{di}{dt} + \frac{(R + r) i}{L} - \frac{E}{L} = 0$$

وهذا يطابق العلاقة المطلوبة.

ـ ما المقصود بثابت الزمن $\tau$ في الدارة الكهربائية؟
ثابت الزمن $\tau$ يُعرَّف على النحو التالي:

$$\tau = \frac{L}{R + r}$$

حيث:

• $L$: الذاتية (Inductance) (بوحدة الهنري).
• $R$: المقاومة الخارجية في الدائرة (بوحدة الأوم).
• $r$: المقاومة الداخلية للمولد أو الوشيعة (بوحدة الأوم).

يمثل $\tau$ الزمن اللازم للوصول إلى حوالي $63\%$ من التغير النهائي في الاستجابة الزمنية للدارة عند تطبيق توتر، أو تيار جديد.

ـ اثبت أن $i(t) = I \left( 1 - e^{-\frac{t}{\tau}} \right)$ يمثل حلًا للمعادلة التفاضلية السابقة:

لدينا:

• $$i(t) = I \left( 1 - e^{-\frac{t}{\tau}} \right)$$
  
• نحسب المشتقة بالنسبة للزمن $\frac{di}{dt}$: $$\frac{di}{dt}=\frac{I}{\tau }{e}^{-\frac{t}{\mathrm{\tau }}}$$

بالتعويض في المعادلة التفاضلية و الاختزال نجد:

$$\frac{I(R+r)}{L} e^{-\frac{t}{\tau}} - \frac{(R+r)}{L} I e^{-\frac{t}{\tau}} = 0$$

وهكذا يصبح لدينا:

$$\frac{(R+r)}{L} I - \frac{E}{L} = 0$$

لدينا:

$$(R + r) I = E$$

وعليه، نجد:

$$\frac{E}{L} - \frac{E}{L} = 0$$

بناءً على هذه الخطوات، نصل إلى نتيجة 

$0 = 0$، مما يعني أن المعادلة التفاضلية محققة.

إذن $i(t) = I \left( 1 - e^{-\frac{t}{\tau}} \right)$ هو حل للمعادلة التفاضلية.

ـ أرسم بيان الدالة $i(t) = I \left(1 - e^{-\frac{t}{\tau}}\right)$.

عند $t = 0$:

$$i(0) = 0$$

عند $t = \tau$:

$$i(\tau) = 0.63I$$

عند $t = 5\tau$:

$$i(5\tau) \approx I$$

ـ كيف تصبح المعادلة التفاضلية و حلها، في حالة وشيعة صافية، و كذلك عبارة ثابت الزمن:

لدينا المعادلة التفاضلية التالية:

$$\frac{di}{dt} + \frac{(R + r)}{L} \cdot i - \frac{E}{L} = 0$$

أو يمكن كتابتها بشكل معادل:

$$\frac{di}{dt} + \frac{i(t)}{\tau} - \frac{E}{L} = 0$$

حيث أن $\tau = \frac{L}{R + r}$.

الحالة الخاصة عندما $r = 0$:

عندما $r = 0$، تصبح المعادلة التفاضلية:

$$\frac{di}{dt} + \frac{R}{L} \cdot i - \frac{E}{L} = 0$$

أو كتابة المعادلة بشكل معادل:

$$\frac{di}{dt} + \frac{i(t)}{\tau} - \frac{E}{L} = 0$$

حيث أن $\tau = \frac{L}{R}$.

لحل المعادلة باستخدام الشكل 

$i(t) = I \left(1 - e^{-\frac{Rt}{L}}\right)$، نلاحظ أن $i(t)$ يمثل التغير في شدة التيار الكهربائي مع مرور الزمن.

ثابت الزمن $\tau$:

من الحل، نجد أن ثابت الزمن $\tau$ هو:

$$\tau = \frac{L}{R}$$

وبذلك، المعادلة التفاضلية تتخذ الشكل:

$$\frac{di}{dt} + \frac{i(t)}{\tau} - \frac{E}{L} = 0$$

حيث أن ثابت الزمن $\tau$ يعبر عن الزمن الذي يحتاجه التيار للوصول إلى حوالي 63% من قيمته النهائية $I$.

ـ استنتج عبارة فرق الكمون بين طرفي كل من الوشيعة، والمقاومة ؟

ـ أرسم البيان الذي يمثل فرق الكمون (التوتر) في كل حالة ؟

فرق الكمون بين طرفي الوشيعة في حالة دارة مغلقة

في حالة وشيعة غير صافية (r ≠ 0) ودارة مغلقة

لدينا المعادلة:

$$u_B = L \frac{di}{dt} + r \cdot i \tag{*}$$

حيث:

$$i(t) = I \left(1 - e^{-\frac{(R + r)t}{L}}\right)$$

وبإعادة ترتيب المعادلة، نجد:

$$i(t) = I - I e^{-\frac{(R + r)t}{L}} \tag{1}$$

نحسب المشتقة بالنسبة للزمن:

$$\frac{di}{dt} = \frac{I (R + r)}{L} e^{-\frac{(R + r)t}{L}} \tag{2}$$

نقوم الآن بتعويض المعادلتين (1) و (2) في المعادلة (*):

$$u_B = L \cdot \frac{I (R + r)}{L} e^{-\frac{(R + r)t}{L}} + r \cdot I$$

بالتبسيط:

$$u_B = R I e^{-\frac{(R + r)t}{L}} + r I$$

نلاحظ أن:

$$u_B = (u_R)_{\text{max}} e^{-\frac{(R + r)t}{L}} + (u_r)_{\text{max}}$$

حيث:

$$(u_R)_{\text{max}} = R I \quad \text{و} \quad (u_r)_{\text{max}} = r I$$

ثابت الزمن $\tau$:

من خلال تعريف ثابت الزمن $\tau$ كالتالي:

$$\tau = \frac{L}{R + r}$$

نحصل على:

$$u_B = (u_R)_{\text{max}} e^{-\frac{t}{\tau}} + (u_r)_{\text{max}}$$

وهذا هو الشكل النهائي للمعادلة.

رسم بيان u_B في حالة وشيعة غير صافية، ودارة مغلقة:

لدينا:

$$u_B = (u_R)_{\text{max}} e^{-t/\tau} + (u_r)_{\text{max}}$$

حيث:

$$(u_R)_{\text{max}} = RI, \quad (u_r)_{\text{max}} = rI, \quad I = \frac{E}{R + r}$$

• عند $t = 0$:

  $$u_B(0) = (u_R)_{\text{max}} + (u_r)_{\text{max}}$$

• عند $t = \tau$:

  $$u_B(\tau) = (u_R)_{\text{max}} e^{-\tau/\tau} + (u_r)_{\text{max}}$$

  ومنه:

  $$u_B(\tau) = 0.37 (u_R)_{\text{max}} + (u_r)_{\text{max}}$$

• عند $t = 5\tau$:

  $$u_B(5\tau) = (u_R)_{\text{max}} e^{-5\tau/\tau} + (u_r)_{\text{max}}$$

  ومنه:

  $$u_B(5\tau) \approx (u_r)_{\text{max}} = rI$$

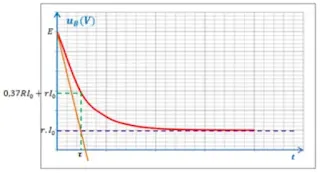
في حالة وشيعة صافية (r = 0) ودارة مغلقة:

عند وضع $r = 0$ في المعادلة:

$$u_B = (u_R)_{\text{max}} e^{-\frac{t}{\tau}} + (u_r)_{\text{max}}$$

نحصل على:

$$(u_R)_{\text{max}} = R \cdot I \quad \text{و} \quad (u_r)_{\text{max}} = 0$$

إذن المعادلة تصبح:

$$u_B = R \cdot I \cdot e^{-\frac{t}{\tau}}$$

وحيث أن $\tau = \frac{L}{R}$، نجد:

$$u_B = R \cdot I \cdot e^{-\frac{Rt}{L}}$$

وبما أن $I = \frac{E}{R}$، فإن المعادلة تصبح:

$$u_B = E \cdot e^{-\frac{Rt}{L}}$$

إذن، عندما $r = 0$، نجد:

$$u_B = E \cdot e^{-\frac{Rt}{L}}$$

طريقة 2:

لدينا المعادلة:

$$\begin{array}{cccc}& u_B=L\frac{di}{dt}& & \text{(*)}\end{array}$$

و لدينا:

$$i(t) = I \left( 1 - e^{-\frac{R t}{L}} \right)$$

أي:

$$i(t) = I - I e^{-\frac{R t}{L}} \tag{1}$$

نحسب المشتقة بالنسبة للزمن:

$$\frac{di}{dt} = \frac{I R}{L} e^{-\frac{R t}{L}} \tag{2}$$

بتعويض (1) في المعادلة (*):

$$u_B = L \cdot \frac{I R}{L} e^{-\frac{R t}{L}}$$

ومنه نجد:

$$u_B=RI{e}^{-\frac{Rt}{L}}$$

لدينا: $I = \frac{E}{R}$، فإذا قمنا بالتعويض في المعادلة:

$$u_B = R \cdot \frac{E}{R} e^{-\frac{R t}{L}}$$

ومنه:

$$u_B=E{e}^{-\frac{Rt}{L}}$$

و حيث أن:

$$\tau = \frac{L}{R}$$

إذن المعادلة تصبح:

$$u_B=E{e}^{-\frac{t}{\tau }}$$

رسم بيان u_B في حالة وشيعة صافية ودارة مغلقة :

لدينا المعادلة:

$$u_B=E{e}^{-\frac{t}{\tau }}$$

عند $t = 0$، نجد:

$$u_B(0) = E e^{-\frac{0}{\tau}} = E \cdot 1 = E$$

عند $t = \tau$، نجد:

$$u_B(\tau) = E e^{-\frac{\tau}{\tau}} = E e^{-1} \approx 0.37 E$$

عند $t = 5\tau$، نجد:

$$u_B(5\tau) = E e^{-\frac{5\tau}{\tau}} = E e^{-5}$$

و منه نجد:

$$u_B(5\tau )\approx 0$$

فرق الكمون بين طرفي المقاومة في حالة دارة مغلقة :

في حالة وشيعة غير صافية (r ≠ 0) ودارة مغلقة :

لدينا:

$$u_R = R \cdot i \tag{1}$$

نعلم أن:

$$i(t) = I - I \cdot e^{-\frac{(R + r)t}{L}} \tag{2}$$

بتعويض 

$i(t)$ من المعادلة (2) في المعادلة (1):

$$u_R = R \cdot \left( I - I \cdot e^{-\frac{(R + r)t}{L}} \right)$$

ومنه:

$$u_R = R \cdot I \cdot \left( 1 - e^{-\frac{(R + r)t}{L}} \right)$$

حيث أن:

$$R \cdot I = (u_R)_{\text{max}}, \quad I = \frac{E}{R + r}, \quad \tau = \frac{L}{R + r}$$

ومنه المعادلة تصبح:

$$u_R=(u_R{)}_{\text{max}}\cdot (1-e^{-\frac{t}{\tau }})$$

رسم بيان u_R في حالة وشيعة غير صافية، ودارة مغلقة:

لدينا:

$$u_R = R \cdot I \cdot \left( 1 - e^{-\frac{t}{\tau}} \right)$$

حيث:

$$I=\frac{E}{R+r}\text{و}\tau =\frac{L}{R+r}$$

نعوض $t = 0$ في المعادلة:

$$u_R(0) = R \cdot I \cdot \left( 1 - e^{-\frac{0}{\tau}} \right)$$$$u_R(0)=R\cdot I\cdot (1-1)=0$$

نعوض $t = \tau$ في المعادلة:

$$u_R(\tau) = R \cdot I \cdot \left( 1 - e^{-\frac{\tau}{\tau}} \right)$$$$u_R(\tau) = R \cdot I \cdot \left( 1 - e^{-1} \right)$$

ومنه:

$$u_R(\tau) = R \cdot I \cdot \left( 1 - 0.37 \right)$$$$u_R(\tau )=R\cdot I\cdot 0.63$$

نعوض $t = 5\tau$ في المعادلة:

$$u_R(5\tau) = R \cdot I \cdot \left( 1 - e^{-\frac{5\tau}{\tau}} \right)$$$$u_R(5\tau) = R \cdot I \cdot \left( 1 - e^{-5} \right)$$

ومنه:

$$u_R(5\tau) \approx R \cdot I \cdot \left( 1 - 0 \right)$$$$u_R(5\tau )\approx R\cdot I$$

في حالة وشيعة صافية (r = 0) ودارة مغلقة:

عند وضع $r = 0$ في المعادلة:

$$u_R = R \cdot I \cdot \left( 1 - e^{-\frac{t}{\tau}} \right)$$

الخطوات:

1. عند $r = 0$، يصبح:

$$I = \frac{E}{R}$$

2. بالتعويض في المعادلة:

$$u_R = R \cdot \frac{E}{R} \cdot \left( 1 - e^{-\frac{t}{\tau}} \right)$$

3. يتم تبسيط المعادلة:

$$u_R = E \cdot \left( 1 - e^{-\frac{t}{\tau}} \right)$$

بما أن:

$$\tau = \frac{L}{R} \quad \text{أي} \quad \frac{1}{\tau} = \frac{R}{L}$$

يمكن كتابة المعادلة أيضًا:

$$u_R = E \cdot \left( 1 - e^{-\frac{R t}{L}} \right)$$

ولكن باستخدام $\tau$ نحصل على الصيغة النهائية:

$$u_R=E\cdot (1-e^{-\frac{t}{\tau }})$$

رسم بيان u_R في حالة وشيعة صافية ودارة مغلقة:

لدينا:

$$u_R=E\cdot (1-e^{-\frac{t}{\tau }})$$

عند $t = 0$، نعوض في المعادلة:

$$u_R(0) = E \cdot \left( 1 - e^{-\frac{0}{\tau}} \right)$$$$u_R(0)=E\cdot (1-1)=0$$

عند $t = \tau$، نعوض في المعادلة:

$$u_R(\tau) = E \cdot \left( 1 - e^{-\frac{\tau}{\tau}} \right)$$$$u_R(\tau) = E \cdot \left( 1 - e^{-1} \right)$$

ومنه:

$$u_R(\tau) = E \cdot \left( 1 - 0.37 \right)$$$$u_R(\tau) = E \cdot 0.63$$

إذن:

$$u_R(\tau )\approx 0.63E$$

عند $t = 5\tau$، نعوض في المعادلة:

$$u_R(5\tau) = E \cdot \left( 1 - e^{-\frac{5\tau}{\tau}} \right)$$$$u_R(5\tau) = E \cdot \left( 1 - e^{-5} \right)$$

ومنه:

$$u_R(5\tau) \approx E \cdot \left( 1 - 0 \right)$$$$u_R(5\tau )\approx E$$

3 ـ 2 ـ حالة فتح القاطعة:

بتطبيق قانون التوترات، وعبارة التوتر بين طرفي الوشيعة، وعبارة التوتر بين طرفي الناقل الأومي

ـ اثبت العلاقة التالية:

$$\frac{di}{dt} + \frac{(R + r)}{L} \cdot i = 0$$

لدينا:

$$u_B + u_R = 0 \tag{1}$$

وأيضًا:

$$u_R = R \cdot i \tag{2}$$

كما أن:

$$u_B = L \frac{di}{dt} + r \cdot i \tag{3}$$

بتعويض المعادلتين $(2)$ و $(3)$ في $(1)$:

$$L \frac{di}{dt} + r \cdot i + R \cdot i = 0$$

ومنه:

$$L \frac{di}{dt} + (R + r) \cdot i = 0$$

بقسمة الطرفين على $L$:

$$\begin{array}{cccc}& \frac{di}{dt}+\frac{(R+r)}{L}\cdot i=0& & \text{(4)}\end{array}$$

ـ ما هي عبارة ثابت الزمن $\tau$ ؟

في الدارة الكهربائية يُعطى بالعلاقة:

$$\tau = \frac{L}{R + r}$$

حيث:

• $L$: الحث الذاتي (Inductance) في الدائرة، ويُقاس بوحدة هنري ($H$).
• $R + r$: المقاومة المكافئة في الدائرة (المقاومة الصرفة $R$ بالإضافة إلى المقاومة الداخلية $r$)، وتُقاس بوحدة الأوم ($\Omega$).

ثابت الزمن $\tau$ يمثل الزمن اللازم لبلوغ التيار، أو التوتر نسبة  $63\%$ من قيمته النهائية في الدائرة.

ـ بين أن:

$$i(t) = I \cdot e^{-t/\tau} \tag{1}$$

هو حل للمعادلة التفاضلية:

$$\frac{di}{dt} + \frac{(R + r)}{L} \cdot i = 0 \tag{4}$$

نحسب المشتقة الأولى لـ $i(t)$:

$$\frac{di}{dt} = -\frac{I \cdot (R + r)}{L} \cdot e^{-t/\tau} \tag{2}$$

بتعويض (1) و (2) في المعادلة (4) و ترتيب حدودها نجد:

$$-\frac{I \cdot (R + r)}{L} \cdot e^{-t/\tau} + \frac{I \cdot (R + r)}{L} \cdot e^{-t/\tau} = 0$$$$0 = 0 \quad \text{(محققة)}$$

إذن:

$$i(t) = I \cdot e^{-t/\tau}$$

يمثل حلاً للمعادلة التفاضلية (4).

ـ ارسم بيان الدالة $i(t) = I \cdot e^{-t/\tau}$ ؟

• عند $t = 0$:

  $$i(0) = I \cdot e^{0} = I$$

• عند $t = \tau$:

  $$i(\tau) = I \cdot e^{-\tau/\tau} = I \cdot e^{-1} \approx 0.37 \cdot I$$

• عند $t = 5\tau$:

  $$i(5\tau) = I \cdot e^{-5\tau/\tau} = I \cdot e^{-5} \approx 0$$

ـ كيف يمكن استنتاج ثابت الزمن τ ؟

يمكن استنتاج ثابت الزمن τ بنفس الطرق السابقة الذكر

ايجاد وحدة ثابت الزمن بالاعتماد على التحليل البعدي:

لدينا:

$$\tau = \frac{L}{R + r}$$

كما أن:

$$u_L = L \cdot \frac{di}{dt} \quad \Rightarrow \quad L = \frac{u_L \cdot dt}{di}$$

ومنه:

$$[L] = [u_L] \cdot [dt] / [di]$$

وبالتالي:

$$[L] = U \cdot T / I \quad \tag{1}$$

وأيضًا:

$$R + r = \frac{E}{I}$$

ومنه:

$$[R + r] = [E]/[I]$$

وبالتالي:

$$[R + r] = U / I \quad \tag{2}$$

من (1) و (2):

$$[\tau] = \frac{[L]}{[R + r]}$$

بالتعويض:

$$[\tau] = \frac{(U \cdot T / I)}{(U / I)}$$

نختصر الوحدات:

$$[\tau] = \frac{U \cdot T \cdot I}{I \cdot U} = T$$

ومنه:
ثابت الزمن $\tau$ يقاس بوحدة الزمن (الثانية).

ـ كيف تصبح عبارة المعادلة التفاضلية، وحلها في حالة، وشيعة صافية، وكذلك عبارة ثابت الزمن τ ؟

لدينا المعادلة التفاضلية:

$$\frac{di}{dt} + \frac{(R + r)}{L} \cdot i(t) = 0$$

أو:

$$\frac{di}{dt} + \frac{i(t)}{\tau} = 0$$

حيث:

$$\tau =\frac{L}{R+r}$$

عند $r = 0$، تصبح المعادلة:

$$\frac{di}{dt} + \frac{R}{L} \cdot i(t) = 0$$

وحل هذه المعادلة التفاضلية هو:

$$i(t) = I \cdot e^{-\frac{R}{L} \cdot t}$$

ثابت الزمن في هذه الحالة:

عند $r = 0$:

$$\tau =\frac{L}{R}$$

ـ استنتج عبارة فرق الكمون بين طرفي كل من الوشيعة والمقاومة ؟

ـ أرسم البيان الذي يمثل فرق الكمون (التوتر) في كل حالة ؟

فرق الكمون بين طرفي الوشيعة في حالة دارة مفتوحة :

في حالة وشيعة غير صافية (r ≠ 0) ودارة مفتوحة :

لدينا:

$$u_B = L \frac{di}{dt} + r \cdot i \tag{*}$$

وأيضًا:

$$i(t) = I \cdot e^{-\frac{(R + r)t}{L}} \tag{1}$$

ومنه:

$$\frac{di}{dt} = -\frac{I \cdot (R + r)}{L} \cdot e^{-\frac{(R + r)t}{L}} \tag{2}$$

بتعويض (1) و (2) في (*):

نبسط الحدود:

$$u_B = -I \cdot (R + r) \cdot e^{-\frac{(R + r)t}{L}} + r \cdot I \cdot e^{-\frac{(R + r)t}{L}}$$$$u_B = -I \cdot R \cdot e^{-\frac{(R + r)t}{L}}$$

حيث:

• $I = \frac{E}{R + r}$
• $\tau = \frac{L}{R + r}$

وبالتالي:

$$u_B = - (u_R)_{\text{max}} \cdot e^{-\frac{t}{\tau}}$$

حيث:

$$(u_R)_{\text{max}} = R \cdot I$$

رسم بيان u_B في حالة وشيعة غير صافية، ودارة مفتوحة :

لدينا:

$$u_B = - (u_R)_{\text{max}} e^{-\frac{t}{\tau}}$$

• عندما $t = 0$:

$$u_B(0) = - (u_R)_{\text{max}}$$

• عندما $t = \tau$:

$$u_B(\tau) = - 0.37 (u_R)_{\text{max}}$$

• عندما $t = 5\tau$:

$$u_B(5\tau) \approx 0$$

في حالة وشيعة صافية (r = 0) ودارة مفتوحة:

عند$r$$=$$0$:

تصبح العلاقة:

$$u_B = - R \cdot I \cdot e^{-\frac{R}{L}t}$$

حيث:

$$I = \frac{E}{R}$$

بتعويض $I$:

$$u_B = - R \cdot \frac{E}{R} \cdot e^{-\frac{R}{L}t}$$

ومنه:

$$u_B=-E\cdot e^{-\frac{t}{\tau }}$$

طريقة 2:

لدينا:

$$u_B = L \cdot \frac{di}{dt} \tag{*}$$

وأيضًا:

$$i(t) = I \cdot e^{-\frac{R}{L}t}$$

حساب $\frac{di}{dt}$:

$$\frac{di}{dt} = -\frac{I \cdot R}{L} \cdot e^{-\frac{R}{L}t} \tag{1}$$

بتعويض (1) في (*):

$$u_B = L \cdot \left(-\frac{I \cdot R}{L} \cdot e^{-\frac{R}{L}t}\right)$$

ومنه:

$$u_B = - R \cdot I \cdot e^{-\frac{R}{L}t}$$

حيث:

• $I = \frac{E}{R}$
• $\tau = \frac{L}{R}$

بتعويض $I$:

$$u_B = - R \cdot \frac{E}{R} \cdot e^{-\frac{t}{\tau}}$$

ومنه:

$$u_B = - E \cdot e^{-\frac{t}{\tau}}$$

ومنه:

$$u_B=-E\cdot e^{-\frac{t}{\tau }}$$

رسم بيان u_B في حالة وشيعة صافية ودارة مفتوحة: 

لدينا:

$$u_B = - E \cdot e^{-\frac{t}{\tau}}$$

عند $t = 0$:

$$u_B(0) = - E$$

عند $t = \tau$:

$$u_B(\tau) = - 0.37E$$

عند $t = 5\tau$:

$$u_B(5\tau) \approx 0$$

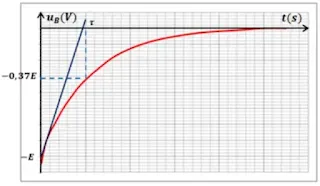
فرق الكمون بين طرفي المقاومة في حالة دارة مفتوحة: 

في حالة وشيعة غير صافية (r ≠ 0) ودارة مفتوحة : 

لدينا:

$$u_R = R \cdot i(t) \tag{1}$$

و لدينا:

$$i(t) = I \cdot e^{-\frac{(R + r)t}{L}} \tag{2}$$

بتعويض (2) في (1):

$$u_R = R \cdot \left(I \cdot e^{-\frac{(R + r)t}{L}}\right)$$$$u_R=R\cdot I\cdot e^{-\frac{(R+r)t}{L}}$$

نعلم أن:

$$I = \frac{E}{R + r}$$$$R \cdot I = R \cdot \frac{E}{R + r}$$$$R \cdot I = \frac{R \cdot E}{R + r}$$

وهذا يمثل التوتر الأعظمي بين طرفي المقاومة:

$$(u_R)_{\text{max}} = \frac{R \cdot E}{R + r}$$

نعلم أن:

$$\frac{R + r}{L} = \frac{1}{\tau}$$

ومنه:

$$u_R=(u_R{)}_{\text{max}}\cdot e^{-\frac{t}{\tau }}$$

رسم بيان u_R في حالة وشيعة غير صافية، ودارة مفتوحة: 

لدينا:

$$u_R = (u_R)_{\text{max}} \cdot e^{-\frac{t}{\tau}}$$

عند $t = 0$:

$$u_R(0) = (u_R)_{\text{max}}$$

عند $t = \tau$:

$$u_R(\tau) = 0.37 \cdot (u_R)_{\text{max}}$$

عند $t = 5\tau$:

$$u_R(5\tau) \approx 0$$

في حالة وشيعة صافية (r = 0) ودارة مفتوحة : 

لدينا:

$$u_R = R \cdot I \cdot e^{-\frac{Rt}{L}}$$

عند $r = 0$:

• نعلم أن:

  $$I = \frac{E}{R}$$

• بالتعويض عن $I$:

  $$u_R = R \cdot \left(\frac{E}{R}\right) \cdot e^{-\frac{Rt}{L}}$$

• ومنه:

  $$u_R = E \cdot e^{-\frac{Rt}{L}}$$

لدينا:

$$\tau = \frac{L}{R}$$

ومنه:

$$\frac{R}{L} = \frac{1}{\tau}$$

ومنه:

$$u_R = E \cdot e^{-\frac{t}{\tau}}$$

رسم بيان u_R في حالة وشيعة صافية، ودارة مفتوحة :

لدينا:

$$u_R = E \cdot e^{-\frac{t}{\tau}}$$

• عندما $t = 0$:

$$u_R(0) = E$$

• عندما $t = \tau$:

$$u_R(\tau) = 0.37 \cdot E$$

• عندما $t = 5\tau$:

$$u_R(5\tau) \approx 0$$

4 ـ الطاقة المخزنة في الوشيعة:

ـ ما هي العبارة اللحظية للطاقة في حالة دارة مغلقة، و في حالة دارة مفتوحة ؟

العبارة اللحظية للطاقة في حالة دارة مغلقة، ووشيعة غير صافية:

لدينا:

$$E_L = \frac{1}{2}L \cdot i^2 \tag{1}$$

ولدينا:

$$i(t) = I \cdot \left(1 - e^{-\frac{t}{\tau}}\right) \tag{2}$$

حيث:

$$I = \frac{E}{R + r}, \quad \tau = \frac{L}{R + r}$$

بتعويض العلاقة (2) في العلاقة (1)، نحصل على:

$$E_L = \frac{1}{2}L \cdot I^2 \cdot \left(1 - e^{-\frac{t}{\tau}}\right)^2$$

العبارة اللحظية للطاقة في حالة دارة مغلقة، ووشيعة صافية :

لدينا:

$$E_L = \frac{1}{2} L I^2 \left(1 - e^{-\frac{t}{\tau}}\right)^2$$

حيث:

$$I = \frac{E}{R}, \quad \tau = \frac{L}{R}$$

العبارة اللحظية للطاقة في حالة دارة مفتوحة، ووشيعة غير صافية: 

لدينا:

$$E_L = \frac{1}{2} L \cdot i^2 \tag{1}$$

ولدينا:

$$i(t) = I \cdot e^{-\frac{t}{\tau}} \tag{2}$$

حيث:

$$I = \frac{E}{R + r}, \quad \tau = \frac{L}{R + r}$$

بتعويض العلاقة (2) في العلاقة (1)، نحصل على:

$$E_L = \frac{1}{2} L \cdot I^2 \cdot e^{-\frac{2t}{\tau}}$$

العبارة اللحظية للطاقة في حالة دارة مفتوحة، ووشيعة صافية: 

لدينا:

$$E_L = \frac{1}{2} L I^2 e^{-\frac{2t}{\tau}}$$

حيث:

$$I = \frac{E}{R}, \quad \tau = \frac{L}{R}$$

ـ أرسم بيان الدالة E_(L) = f(t) ؟

رسم بيان الدالة E_(L) = f(t) في حالة دارة مغلقة، ووشيعة غير صافية: 

لدينا:

$$E_L = \frac{1}{2} L I^2 \left(1 - e^{-\frac{t}{\tau}}\right)^2$$

حيث:

$$I = \frac{E}{R + r}, \quad \tau = \frac{L}{R + r}$$

من أجل توضيح أكثر للرسم، نعتمد على القيم العددية التالية:

• $r = 10 \, \Omega$
• $R = 90 \, \Omega$
• $L = 1 \, \text{H}$

نحسب:

$$\tau = \frac{L}{R + r} = \frac{1}{90 + 10} = 0.01 \, \text{s}$$

ونأخذ:

$$E = 6 \, \text{V}$$

فنجد:

$$I = \frac{E}{R + r} = \frac{6}{90 + 10} = 0.06 \, \text{A}$$

ونحسب الطاقة الاعظمية المخزنة في الوشيعة:

$$E_{L_{\text{max}}} = \frac{1}{2} L I^2 = 1.8 \cdot 10^{-3} \, \text{J}$$

من أجل قيم مختلفة للزمن نحصل على الجدول التالي:

0.02	0.012	0.01	0	t(s)
0.00134	0.0009	0.000716	0	E(L)(J)
0.06	0.05	0.04	0.03	t(s)
0.0018	0.001791	0.00177	0.00162	E(L)(J)

ومنه نحصل على البيان التالي: 

رسم بيان الدالة E_(L) = f(t) في حالة دارة مغلقة، ووشيعة صافية:

لدينا:

$$E_L = \frac{1}{2} L I^2 \left(1 - e^{-\frac{t}{\tau}}\right)^2$$

حيث:

$$I = \frac{E}{R}, \quad \tau = \frac{L}{R}$$

من أجل توضيح أكثر للرسم، نعتمد على القيم العددية التالية:

• $R = 100 \, \Omega$
• $L = 1 \, \text{H}$

نحسب:

$$\tau = \frac{L}{R} = \frac{1}{100} = 0.01 \, \text{s}$$

ونأخذ:

$$E = 6 \, \text{V}$$

فنجد:

$$I = \frac{E}{R} = \frac{6}{100} = 0.06 \, \text{A}$$

ونحسب أقصى طاقة مخزنة في الوشيعة:

$$E_{L_{\text{max}}}=\frac{1}{2}L{I}^2=1.8\cdot 10^{-3}\text{J}$$

من أجل قيم مختلفة للزمن نحصل على الجدول التالي:

0.02	0.012	0.01	0	t(s)
0.00134	0.0009	0.000716	0	E(L)(J)
0.06	0.05	0.04	0.03	t(s)
0.0018	0.001791	0.00177	0.00162	E(L)(J)

ومنه نحصل على البيان التالي:

رسم بيان الدالة E_(L) = f(t) في حالة دارة مفتوحة، ووشيعة غير صافية:

لدينا:

$$E_L = \frac{1}{2} L I^2 e^{-\frac{2t}{\tau}}$$

حيث:

$$I = \frac{E}{R + r}, \quad \tau = \frac{L}{R + r}$$

من أجل توضيح أكثر للرسم، نعتمد على القيم العددية التالية:

• $r = 10 \, \Omega$
• $R = 90 \, \Omega$
• $L = 1 \, \text{H}$

نحسب:

$$\tau = \frac{L}{R + r} = \frac{1}{90 + 10} = 0.01 \, \text{s}$$

ونأخذ:

$$E = 6 \, \text{V}$$

فنجد:

$$I = \frac{E}{R + r} = \frac{6}{90 + 10} = 0.06 \, \text{A}$$

ونحسب أقصى طاقة مخزنة في الوشيعة:

$$E_{L_{\text{max}}} = \frac{1}{2} L I^2 = 1.8 \cdot 10^{-3} \, \text{J}$$

من أجل قيم مختلفة للزمن نحصل على الجدول التالي:

0.02	0.01	0.003465	0	t(s)
0.033	0.245	0.9	1.8	E(L)(×10-3J)
0.06	0.05	0.04	0.03	t(s)
0	8.42E-05	0.000618	0.0045	E(L)(×10-3J)

ومنه نحصل على البيان التالي:

رسم بيان الدالة E_(L) = f(t) في حالة دارة مفتوحة، ووشيعة صافية:

لدينا:

$$E_L = \frac{1}{2} L I^2 e^{-\frac{2t}{\tau}}$$

حيث:

$$I = \frac{E}{R}, \quad \tau = \frac{L}{R}$$

من أجل توضيح أكثر للرسم، نعتمد على القيم العددية التالية:

• $R = 100 \, \Omega$
• $L = 1 \, \text{H}$

نحسب:

$$\tau = \frac{L}{R} = \frac{1}{100} = 0.01 \, \text{s}$$

ونأخذ:

$$E = 6 \, \text{V}$$

فنجد:

$$I = \frac{E}{R} = \frac{6}{100} = 0.06 \, \text{A}$$

ونحسب أقصى طاقة مخزنة في الوشيعة:

$$E_{L_{\text{max}}} = \frac{1}{2} L I^2 = 1.8 \cdot 10^{-3} \, \text{J}$$

من أجل قيم مختلفة للزمن نحصل على الجدول التالي:

0.02	0.01	0.003465	0	t(s)
0.033	0.245	0.9	1.8	E(L)(×10-3J)
0.06	0.05	0.04	0.03	t(s)
0	8.42E-05	0.000618	0.0045	E(L)(×10-3J)

ومنه نحصل على البيان التالي:

ـ استنتج  زمن تناقص الطاقة إلى النصف ؟

في حالة الدارة المفتوحة لدينا:

$$E_L = \frac{1}{2} L I^2 e^{-\frac{2t}{\tau}}$$

ومنه:

$$E_{L_{\text{max}}} = E_L(0) = \frac{1}{2} L I^2$$

وعند الزمن $t_{1/2}$، لدينا:

$$E_L(t_{1/2}) = \frac{1}{2} L I^2 e^{-\frac{2t_{1/2}}{\tau}} \tag{1}$$

ومن جهة أخرى:

$$E_L(t_{1/2}) = \frac{1}{2} \cdot \frac{1}{2} L I^2 = \frac{1}{4} L I^2 \tag{2}$$

بالمساواة بين (1) و (2)، نجد:

$$\frac{1}{2} L I^2 e^{-\frac{2t_{1/2}}{\tau}} = \frac{1}{4} L I^2$$

ومنه:

$$e^{-\frac{2t_{1/2}}{\tau}} = \frac{1}{2}$$

بأخذ اللوغاريتم الطبيعي للطرفين:

$$\ln\left(e^{-\frac{2t_{1/2}}{\tau}}\right) = \ln\left(\frac{1}{2}\right)$$

ومنه:

$$-\frac{2t_{1/2}}{\tau} = \ln(2)$$

وأخيرًا:

$$t_{1\mathrm{/}2}=\frac{\tau \ln (2)}{2}$$

ملاحظة :

يمكن ايجاد زمن تزايد الطاقة الى النصف في حالة الدارة المغلقة كما يلي :

لدينا:

$$E_L = \frac{1}{2} L I^2 \left(1 - e^{-\frac{t}{\tau}}\right)^2$$

ومنه:

$$E_{L_{\text{max}}} = \frac{1}{2} L I^2$$

وعند الزمن $t_{1/2}$، لدينا:

$$E_L(t_{1/2}) = \frac{1}{2} L I^2 \left(1 - e^{-\frac{t_{1/2}}{\tau}}\right)^2 \tag{1}$$

ومن جهة أخرى:

$$E_L(t_{1/2}) = \frac{1}{2} \cdot \frac{1}{2} L I^2 = \frac{1}{4} L I^2 \tag{2}$$

بالمساواة بين (1) و (2)، نجد:

$$\frac{1}{2} L I^2 \left(1 - e^{-\frac{t_{1/2}}{\tau}}\right)^2 = \frac{1}{4} L I^2$$

ومنه:

$$\left(1 - e^{-\frac{t_{1/2}}{\tau}}\right)^2 = \frac{1}{2}$$

بأخذ الجذر التربيعي للطرفين:

$$1 - e^{-\frac{t_{1/2}}{\tau}} = \sqrt{\frac{1}{2}} = 0.707$$

ومنه:

$$- e^{-\frac{t_{1/2}}{\tau}} = -0.293$$

بأخذ اللوغاريتم الطبيعي للطرفين:

$$\ln\left(e^{-\frac{t_{1/2}}{\tau}}\right) = \ln(0.293)$$

ومنه:

$$-\frac{t_{1/2}}{\tau} = \ln(0.293) = -1.227$$

وأخيرًا:

$$t_{1/2} = 1.227 \cdot \tau$$

اقرأ الظواهر الكهربائية

اقرأ الظواهر الكهربائية. دراسة ثنائي القطب RC

اقرأ المعادلة التفاضلية للدارة RC بدلالة الشحنة

اقرأ المعادلات التفاضلية للدارة RL

وثيقة التلميذ بصيغة الـ PDF